设函数f(x)=alnx-bx2(x>0),
(1)若函数f(x)在x=1处与直线y=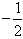 相切,
相切,
①求实数a,b的值;
②求函数f(x)在[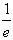 ,e]上的最大值;
,e]上的最大值;
(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[0,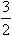 ],x∈(1,e2]都成立,求实数m的取值范围。
],x∈(1,e2]都成立,求实数m的取值范围。
(1)若函数f(x)在x=1处与直线y=
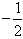 相切,
相切,①求实数a,b的值;
②求函数f(x)在[
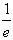 ,e]上的最大值;
,e]上的最大值;(2)当b=0时,若不等式f(x)≥m+x对所有的a∈[0,
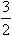 ],x∈(1,e2]都成立,求实数m的取值范围。
],x∈(1,e2]都成立,求实数m的取值范围。 解:(1)①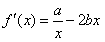 ,
,
∵函数f(x)在x=1处与直线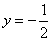 相切,
相切,
∴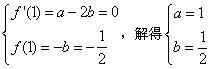 ;
;
②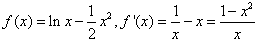 ,
,
当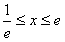 时,令f′(x)>0,得
时,令f′(x)>0,得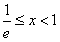 ;
;
令f′(x)<0,得1<x≤e,
∴f(x)在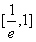 上单调递增,在[1,e]上单调递减,
上单调递增,在[1,e]上单调递减,
∴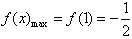 ;
;
(2)当b=0时,f(x)=alnx,
若不等式f(x)≥m+x对所有的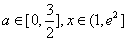 都成立,
都成立,
则alnx≥m+x对所有的 都成立,
都成立,
即m≤alnx-x对所有的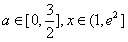 都成立,
都成立,
令h(a)=alnx-x,则h(a)为一次函数,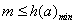 ,
,
∵x∈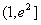 ,∴lnx>0,
,∴lnx>0,
∴h(a)在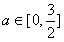 上单调递增,∴
上单调递增,∴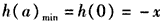 ,
,
∴m≤-x对所有的x∈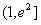 都成立,
都成立,
∵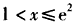 ,
,
∴ ,∴
,∴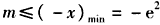 。
。

