【题目】已知四棱锥的底面ABCD是边长为2的正方形，且.若四棱锥P-ABCD的五个顶点在以4为半径的同一球面上，当PA最长时，则______________；四棱锥P-ABCD的体积为______________.

【答案】90°

【解析】

易得平面PAD，P点在与BA垂直的圆面内运动，显然，PA是圆的直径时，PA最长；将四棱锥补形为长方体，易得为球的直径即可得到PD，从而求得四棱锥的体积.

如图，由及，得平面PAD，

即P点在与BA垂直的圆面内运动，

易知，当P、、A三点共线时，PA达到最长，

此时，PA是圆的直径，则；

又，所以平面ABCD，

此时可将四棱锥补形为长方体，

其体对角线为，底面边长为2的正方形，

易求出，高，

故四棱锥体积.

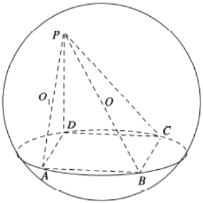
故答案为： (1) 90° ； (2) .

关闭