【题目】已知函数f(x)![]() |2x﹣3|,g(x)
|2x﹣3|,g(x)![]() |2x+a+b|.
|2x+a+b|.
(1)解不等式f(x)![]() x2;
x2;
(2)当a![]() 0,b
0,b![]() 0时,若F(x)
0时,若F(x)![]() f(x)+g(x)的值域为[5,+∞),求证:
f(x)+g(x)的值域为[5,+∞),求证:![]() .
.
【答案】(1)![]() 或
或![]() ;(2)见解析
;(2)见解析
【解析】
(1)由题意可得|2x﹣3|![]() x2,由绝对值的意义,去绝对值,解不等式,求并集,可得所求解集;
x2,由绝对值的意义,去绝对值,解不等式,求并集,可得所求解集;
(2)由a![]() 0,b
0,b![]() 0,根据绝对值三角不等式,化简可得F(x)的最小值,可得a+b的值,再由乘1法和基本不等式,即可得证.
0,根据绝对值三角不等式,化简可得F(x)的最小值,可得a+b的值,再由乘1法和基本不等式,即可得证.
(1)解:不等式f(x)![]() x2化为|2x﹣3|
x2化为|2x﹣3|![]() x2,等价于
x2,等价于 或
或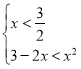 ,
,
即为![]() 或
或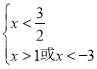 ,
,
解得x![]() 或x
或x![]() ﹣3或1
﹣3或1![]() x
x![]() ,
,
所以不等式f(x)![]() x2的解集为{x|x
x2的解集为{x|x![]() 1或x
1或x![]() ﹣3};
﹣3};
(2)证明:由a![]() 0,b
0,b![]() 0,
0,
根据绝对值三角不等式可知F(x)![]() f(x)+g(x)
f(x)+g(x)![]() |2x﹣3|+|2x+a+b|
|2x﹣3|+|2x+a+b|![]() |3﹣2x|+|2x+a+b|
|3﹣2x|+|2x+a+b|
≥|3﹣2x+2x+a+b|![]() |a+b+3|
|a+b+3|![]() a+b+3,
a+b+3,
又F(x)![]() f(x)+g(x)的值域为[5,+∞),
f(x)+g(x)的值域为[5,+∞),
可得a+b+3![]() 5,
5,
即a+b![]() 2,
2,
即(a+2)+(b+2)![]() 6,
6,
故![]() [(a+2)+(b+2)](
[(a+2)+(b+2)](![]() )
)
![]() (2
(2![]() )
)![]() (2+2
(2+2![]() )
)![]() ,
,
当且仅当![]() ,即a
,即a![]() b
b![]() 1时取等号时,
1时取等号时,
故![]() .
.

