已知A(1,1)为椭圆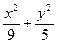 =1内一点,F1为椭圆左焦点,P为椭圆上一动点
=1内一点,F1为椭圆左焦点,P为椭圆上一动点 求|PF1|+|PA|的最大值和最小值.
求|PF1|+|PA|的最大值和最小值.
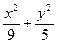 =1内一点,F1为椭圆左焦点,P为椭圆上一动点
=1内一点,F1为椭圆左焦点,P为椭圆上一动点 求|PF1|+|PA|的最大值和最小值.
求|PF1|+|PA|的最大值和最小值.|PF1|+|PA|的最大值是6+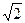 ,最小值是6–
,最小值是6–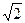
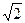 ,最小值是6–
,最小值是6–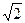
由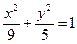 可知a=3,b=
可知a=3,b=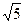 ,c=2,左焦点F1(–2,0),右焦点F2(2,0)
,c=2,左焦点F1(–2,0),右焦点F2(2,0) 由椭圆定义,|PF1|=2a–|PF2|=6–|PF2|,
由椭圆定义,|PF1|=2a–|PF2|=6–|PF2|,
∴|PF1|+|PA|=6–|PF2|+|PA|=6+|PA|–|PF2|
如图:

由||PA|–|PF2||≤|AF2|=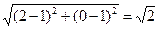 知
知
–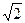 ≤|PA|–|PF2|≤
≤|PA|–|PF2|≤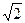 .
.
当P在AF2延长线上的P2处时,取右“=”号;
当P在AF2的反向延长线的P1处时,取左“=”号.
即|PA|–|PF2|的最大、最小值分别为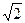 ,–
,–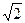 .
.
于是|PF1|+|PA|的最大值是6+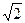 ,最小值是6–
,最小值是6–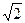 .
.
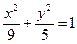 可知a=3,b=
可知a=3,b=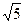 ,c=2,左焦点F1(–2,0),右焦点F2(2,0)
,c=2,左焦点F1(–2,0),右焦点F2(2,0) 由椭圆定义,|PF1|=2a–|PF2|=6–|PF2|,
由椭圆定义,|PF1|=2a–|PF2|=6–|PF2|,∴|PF1|+|PA|=6–|PF2|+|PA|=6+|PA|–|PF2|
如图:

由||PA|–|PF2||≤|AF2|=
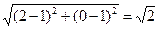 知
知–
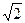 ≤|PA|–|PF2|≤
≤|PA|–|PF2|≤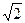 .
.当P在AF2延长线上的P2处时,取右“=”号;
当P在AF2的反向延长线的P1处时,取左“=”号.
即|PA|–|PF2|的最大、最小值分别为
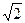 ,–
,–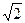 .
.于是|PF1|+|PA|的最大值是6+
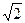 ,最小值是6–
,最小值是6–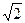 .
. 
