集合A={x|（x+1）（x-2）＜0}，B={x|（x+2）（x-a）≤0}，若A∩B=A，则a的取值范围是


  1. A.
    a＜-1
  2. B.
    a＞2
  3. C.
    a≥2
  4. D.
    -1＜a＜2
C
分析：化简集合A，根据A∩B=A，可得 A⊆B，考查集合端点间的大小关系，从而求得a的取值范围．
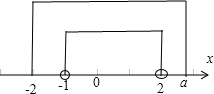
解答：∵集合A={x|（x+1）（x-2）＜0}={x|-1＜x＜2}，B={x|（x+2）（x-a）≤0}，A∩B=A，
∴A⊆B，a≥2，
故选C．

点评：本题主要考查集合中参数的取值问题，两个集合的交集的定义，体现了数形结合的数学思想，属于中档题．
关闭