【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA= ![]() ,cosC=
,cosC= ![]()
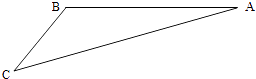
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
参考答案:
【答案】
(1)解:在△ABC中,因为cosA= ![]() ,cosC=
,cosC= ![]() ,所以sinA=
,所以sinA= ![]() ,sinC=
,sinC= ![]() ,
,
从而sinB=sin[π﹣(A+C)]=sin(A+C)=sinAcosC+cosAsinC= ![]() =
= ![]()
由正弦定理 ![]() ,得AB=
,得AB= ![]() =
= ![]() =1040m.
=1040m.
所以索道AB的长为1040m.
(2)解:假设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,所以由余弦定理得
d2=(100+50t)2+(130t)2﹣2×130t×(100+50t)× ![]() =200(37t2﹣70t+50)=200[37(t﹣
=200(37t2﹣70t+50)=200[37(t﹣ ![]() )2+
)2+ ![]() ],
],
因0≤t≤ ![]() ,即0≤t≤8,故当t=
,即0≤t≤8,故当t= ![]() min时,甲、乙两游客距离最短
min时,甲、乙两游客距离最短
(3)解:由正弦定理 ![]() ,得BC=
,得BC= ![]() =
= ![]() =500m,
=500m,
乙从B出发时,甲已经走了50×(2+8+1)=550m,还需走710m才能到达C.
设乙步行的速度为 v m/min,由题意得﹣3≤ ![]() ≤3,解得
≤3,解得 ![]() ,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在[
,所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在[ ![]() ]范围内
]范围内
【解析】(1)根据正弦定理即可确定出AB的长;(2)设乙出发t分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,由余弦定理可得;(3)设乙步行的速度为 v m/min,从而求出v的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 ,
,  (
( ).
).(Ⅰ)求函数
 的单调区间;
的单调区间;(Ⅱ)若函数
 在
在 处取得极大值,求正实数
处取得极大值,求正实数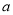 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
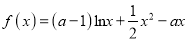 (
(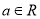 )
)(1)讨论
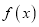 的单调性;
的单调性;(2)设
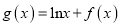 ,若
,若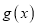 有两个极值点
有两个极值点 ,且不等式
,且不等式 恒成立,求实数
恒成立,求实数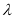 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在学校体育节中,某班全体40名同学参加跳绳、踢毽子两项比赛的人数统计如下:
参加跳绳的同学
未参加跳绳的同学
参加踢毽的同学
9
4
未参加踢毽的同学
7
20
(1)从该班随机选1名同学,求该同学至少参加上述一项活动的概率;
(2)已知既参加跳绳又参加踢毽的9名同学中,有男生5名,女生4名,现从这5名男生,4名女生中各随机挑选1人,求男同学甲未被选中且女同学乙被选中的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
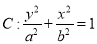 (
(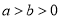 )的离心率为
)的离心率为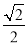 ,点
,点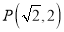 在椭圆上
在椭圆上(1)求椭圆
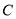 的方程;
的方程;(2)过椭圆上的焦点
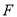 作两条相互垂直的弦
作两条相互垂直的弦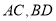 ,求
,求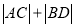 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设Sn是数列{an}的前n项和,且2an+Sn=An2+Bn+C.
(1)当A=B=0,C=1时,求an;
(2)若数列{an}为等差数列,且A=1,C=﹣2. ①设bn=2nan , 求数列{bn}的前n项和;
②设cn=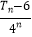 ,若不等式cn≥
,若不等式cn≥ 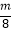 对任意n∈N*恒成立,求实数m的取值范围.
对任意n∈N*恒成立,求实数m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
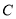 过
过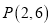 ,
, 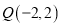 两点,且圆心
两点,且圆心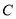 在直线
在直线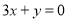 上.
上.(1)求圆
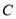 的方程;
的方程;(2)若直线
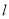 过点
过点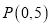 且被圆
且被圆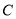 截得的线段长为
截得的线段长为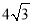 ,求
,求 的方程.
的方程.
相关试题

