【题目】已知点![]() ,动点
,动点![]() ,
, ![]() 分别在
分别在![]() 轴,
轴, ![]() 轴上运动,
轴上运动, ![]() ,
, ![]() 为平面上一点,
为平面上一点, ![]() ,过点
,过点![]() 作
作![]() 平行于
平行于![]() 轴交
轴交![]() 的延长线于点
的延长线于点![]() .
.
(Ⅰ)求点![]() 的轨迹曲线
的轨迹曲线![]() 的方程;
的方程;
(Ⅱ)过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
, ![]() 分别交曲线
分别交曲线![]() 于
于![]() ,
, ![]() 两点(直线
两点(直线![]() 不过
不过![]() ),交
),交![]() 于
于![]() ,
, ![]() 两点.若线段
两点.若线段![]() 中点的轨迹方程为
中点的轨迹方程为![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
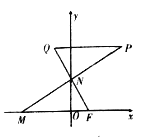
参考答案:
【答案】(1)![]() ;(2)2.
;(2)2.
【解析】试题分析:(Ⅰ)由题意可得![]() 为
为![]() ,
, ![]() 的中点,设
的中点,设![]() ,则
,则![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,结合
,结合![]() 可得点
可得点![]() 的轨迹方程;(Ⅱ)设直线
的轨迹方程;(Ⅱ)设直线![]() 与
与![]() 轴的交点
轴的交点![]() ,设
,设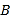 ,
, 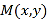 ,
, ![]() ,
, ![]() 中点为
中点为![]() , 当当
, 当当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 可得
可得![]() ,当
,当![]() 与
与![]() 轴垂直时也适合方程,由题意得
轴垂直时也适合方程,由题意得![]() 即为
即为![]() 的准线,结合面积公式即可.
的准线,结合面积公式即可.
试题解析:(Ⅰ)设![]() ,由
,由![]() 为
为![]() ,
, ![]() 的中点可得
的中点可得![]() 为
为![]() ,
, ![]() 的中点,则
的中点,则![]() ,
, ![]() 分别为
分别为![]() ,
, ![]() ,
,![]() ,
, ![]()
![]() 可得点
可得点![]() 的轨迹方程为:
的轨迹方程为: ![]()
(Ⅱ)设直线![]() 与
与![]() 轴的交点
轴的交点![]() ,设
,设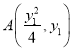 ,
, 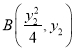
设![]() ,
, ![]() 中点为
中点为![]() ,
,
当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() 可得
可得![]()
而![]() ,则
,则![]() 即
即![]() ,即
,即![]()
当![]() 与
与![]() 轴垂直时,
轴垂直时, ![]() ,
, ![]() 中点
中点![]() 与
与![]() 重合,适合方程.
重合,适合方程.
由![]() 为
为![]() ,
, ![]() 的中点,可知过
的中点,可知过![]() 点作
点作![]() 轴的垂线
轴的垂线![]() 即为
即为![]() 的准线,
的准线,
![]() ,
, ![]()
![]()
![]() 与
与![]() 的面积之比为2.
的面积之比为2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
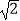 sin(2x+
sin(2x+  ),给出下列四个命题:
),给出下列四个命题:
①函数f(x)在区间[ ,
, 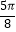 ]上是减函数;
]上是减函数;
②直线x= 是f(x)的图象的一条对称轴;
是f(x)的图象的一条对称轴;
③函数f(x)的图象可以由函数y=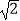 sin2x的图象向左平移
sin2x的图象向左平移  而得到;
而得到;
④函数f(x)的图象的一个对称中心是(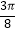 ,0).
,0).
其中正确的个数是( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列命题:
①在△ABC中,若A<B,则sinA<sinB;
②在同一坐标系中,函数y=sinx与y=lgx的交点个数为2个;
③函数y=|tan2x|的最小正周期为 ;
;
④存在实数x,使2sin(2x﹣ )﹣1=
)﹣1=  成立;
成立;
其中正确的命题为(写出所有正确命题的序号). -
科目: 来源: 题型:
查看答案和解析>>【题目】下表是某校高三一次月考5个班级的数学、物理的平均成绩:
班级
1
2
3
4
5
数学(
 分)
分)111
113
119
125
127
物理(
 分)
分)92
93
96
99
100
(Ⅰ)一般来说,学生的物理成绩与数学成绩具有线性相关关系,根据上表提供的数据,求两个变量
 ,
,  的线性回归方程
的线性回归方程 ;
;(Ⅱ)从以上5个班级中任选两个参加某项活动,设选出的两个班级中数学平均分在115分以上的个数为
 ,求
,求 的分布列和数学期望.
的分布列和数学期望.附:
 ,
, 
-
科目: 来源: 题型:
查看答案和解析>>【题目】下表提供了某厂节能降耗技术改造后生产产品过程中记录的产量x(吨)与相应的生产能耗y(吨)标准煤的几组对照数据:
x
3
4
5
6
y
2.5
3
4
4.5
(1)求y关于x的线性回归方程;(已知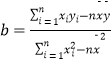 )
)
(2)已知该厂技术改造前100吨甲产品能耗为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技术改造前降低了多少吨标准煤. -
科目: 来源: 题型:
查看答案和解析>>【题目】某家电公司销售部门共有200位销售员,每位部门对每位销售员都有1400万元的年度销售任务,已知这200位销售员去年完成销售额都在区间
 (单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为
(单位:百万元)内,现将其分成5组,第1组,第2组,第3组,第4组,第5组对应的区间分别为 ,
,  ,
,  ,
,  ,
,  ,绘制出频率分布直方图.
,绘制出频率分布直方图.
(1)求
 的值,并计算完成年度任务的人数;
的值,并计算完成年度任务的人数;(2)用分层抽样从这200位销售员中抽取容量为25的样本,求这5组分别应抽取的人数;
(3)现从(2)中完成年度任务的销售员中随机选取2位,奖励海南三亚三日游,求获得此奖励的2位销售员在同一组的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某企业为了解下属某部门对本企业职工的服务情况,随机访问50名职工,根据这50名职工对该部门的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为[40,50],[50,60],…,[80,90],[90,100]
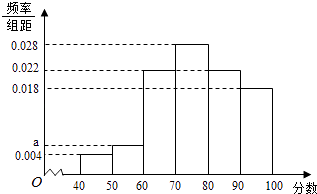
(1)求频率分布图中a的值;
(2)估计该企业的职工对该部门评分不低于80的概率;
(3)从评分在[40,60]的受访职工中,随机抽取2人,求此2人评分都在[40,50]的概率.
相关试题

