【题目】已知函数![]() ,
,![]() 是实数.
是实数.
(1)若函数![]() 是定义在
是定义在![]() 上的奇函数,求
上的奇函数,求![]() 的值,并求方程
的值,并求方程![]() 的解;
的解;
(2)若![]() 对任意的
对任意的![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
(3)若![]() ,方程
,方程![]() 有解,求实数
有解,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;
;
(2)![]() ;
;
(3)![]() 或
或![]() ;
;
【解析】
(1)可根据奇函数性质![]() ,也可根据特殊点
,也可根据特殊点![]() 求
求![]() ,再进行验证即可;令
,再进行验证即可;令![]() 结合一元二次方程的解法即可求解;
结合一元二次方程的解法即可求解;
(2)可采用分离常数法得![]() 对任意的
对任意的![]() 恒成立,令
恒成立,令![]() ,
,![]() ,令
,令![]() ,则
,则![]() ,结合二次函数性质即可求解;
,结合二次函数性质即可求解;
(3)![]() 时,
时,![]() ,
,![]() 化简得
化简得![]() ,采用构造函数法,令
,采用构造函数法,令![]() ,转化为方程
,转化为方程![]() 在
在![]() 上有解,再结合二次函数对称轴与增减性进一步求解即可
上有解,再结合二次函数对称轴与增减性进一步求解即可
(1)方法一:因为函数![]() 是定义在
是定义在![]() 上的奇函数,
上的奇函数,
所以![]() 对任意
对任意![]() 恒成立,
恒成立,
即![]() 对任意
对任意![]() 恒成立,
恒成立,
整理得![]() 对任意
对任意![]() 恒成立,
恒成立,
所以![]() .
.
方法二:因为函数![]() 是定义在
是定义在![]() 上的奇函数,所以
上的奇函数,所以![]() ,解得
,解得![]()
检验:当![]() 时,
时,![]() ,
,
此时,![]()
所以![]()
此时![]() .
.
因为![]() ,即
,即![]() ,整理得
,整理得![]()
解得![]() 或
或![]() (舍).
(舍).
所以![]() .
.
(2)因为![]() 对任意的
对任意的![]() 恒成立,
恒成立,
所以![]() ,即
,即![]() 对任意的
对任意的![]() 恒成立.
恒成立.
令![]() ,则
,则![]() ,
,
令![]() ,所以
,所以![]()
![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
所以![]() ,所以
,所以![]() .
.
(3)当![]() 时,
时,![]() ,因为
,因为![]() ,
,
所以![]() .
.
令![]() ,则
,则![]() ,
,
转化为方程![]() 在
在![]() 上有解.
上有解.
令![]() ,
,
①当![]() 时,
时,![]() 在
在![]() 为增函数
为增函数
所以![]() ,得
,得![]() .
.
②当![]() 时,需
时,需![]() ,
,
即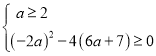 ,解得
,解得![]() ,
,
所以![]() 或
或![]() .
.

