【题目】已知向量a=(cos α,sin α),b=(cos β,sin β),c=(-1,0).
(1) 求向量b+c的模的最大值;
(2) 若α=![]() ,且a⊥(b+c),求cos β的值.
,且a⊥(b+c),求cos β的值.
参考答案:
【答案】(1)2(2)见解析
【解析】试题分析(1)根据向量加法坐标表示以及向量模的坐标表示可得|b+c|2=2(1-cos β),再根据三角函数有界性可得模的最值(2)由向量垂直可得数量积为零,根据向量数量积坐标表示可得关于β的方程,解得β值 ,即得cos β的值.
试题解析:解:(1) b+c=(cos β-1,sin β),则|b+c|2=(cos β-1)2+sin2β=2(1-cos β).
∵ -1≤cos β≤1,
∴ 0≤|b+c|2≤4,即0≤|b+c|≤2.
当cos β=-1时,|b+c|取最大值2,
∴ 向量b+c的模的最大值为2.
(2) ∵ b+c=(cos β-1,sin β),
∴ a·(b+c)=cos αcos β-cos α+sin αsin β
=cos(α-β)-cos α.
∵ a⊥(b+c),
∴ a·(b+c)=0,即cos(α-β)=cos α.
又α=![]() ,∴ cos
,∴ cos![]() =cos
=cos![]() ,β-
,β-![]() =2kπ±
=2kπ±![]() (k∈Z),
(k∈Z),
∴ β=2kπ+![]() 或β=2kπ,k∈Z,
或β=2kπ,k∈Z,
∴ cos β=0或cos β=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{
 }的前n项和
}的前n项和 (n为正整数)。
(n为正整数)。(1)令
 ,求证数列{
,求证数列{ }是等差数列,并求数列{
}是等差数列,并求数列{ }的通项公式;
}的通项公式;(2)令
 ,
,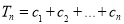 试比较
试比较 与
与 的大小,并予以证明.
的大小,并予以证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
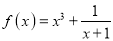 ,
, 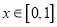 .
.(1)证明:
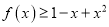 ;
;(2)根据(1)证明:
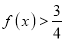 .
.(B)已知函数
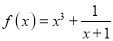 ,
, 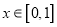 .
.(1)用分析法证明:
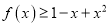 ;
;(2)证明:
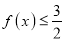 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】等比数列
 的前
的前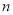 项和为
项和为 ,已知对任意的
,已知对任意的 ,点
,点 均在函数
均在函数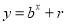 (
( 且
且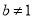 ,
,  均为常数)的图象上.
均为常数)的图象上.
(1)求 的值;
的值;(2)当
 时,记
时,记 ,证明:对任意的
,证明:对任意的 ,不等式
,不等式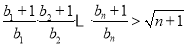 成立.
成立. -
科目: 来源: 题型:
查看答案和解析>>【题目】统计表明,某种型号的汽车在匀速行驶中每小时耗油量
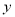 (升)关于行驶速度
(升)关于行驶速度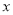 (千米/小时)的函数解析式可以表示为:
(千米/小时)的函数解析式可以表示为: 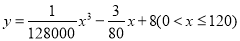 ,已知甲、乙两地相距100千米.
,已知甲、乙两地相距100千米.(1)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(2)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
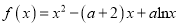 .
.(Ⅰ)当
 时,求函数
时,求函数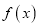 的极小值;
的极小值;(Ⅱ)当
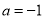 时,过坐标原点
时,过坐标原点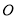 作曲线
作曲线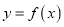 的切线,设切点为
的切线,设切点为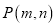 ,求实数
,求实数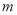 的值;
的值;(Ⅲ)设定义在
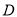 上的函数
上的函数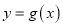 在点
在点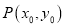 处的切线方程为
处的切线方程为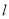 :
: 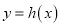 ,当
,当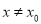 时,若
时,若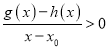 在
在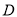 内恒成立,则称
内恒成立,则称 为函数
为函数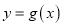 的“转点”.当
的“转点”.当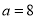 时,试问函数
时,试问函数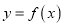 是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由.
是否存在“转点”.若存在,请求出“转点”的横坐标,若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】一个几何体的三视图如下图所示,其中主视图与左视图是腰长为6的等腰直角三角形,俯视图是正方形.

(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD—A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD—A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面角的余弦值.
相关试题

