【题目】随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调查,并统计得出某款车的使用年限![]() (单位:年)与所支出的总费用
(单位:年)与所支出的总费用![]() (单位:万元)有如下的数据资料:
(单位:万元)有如下的数据资料:
使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知![]() 对
对![]() 呈线性相关关系.
呈线性相关关系.
(1)试求线性回归方程![]() =
=![]()
![]() +
+![]() 的回归系数
的回归系数![]() ,
,![]() ;
;
(2)当使用年限为![]() 年时,估计车的使用总费用.
年时,估计车的使用总费用.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】试题分析:(1)列表求得![]() =4,
=4, ![]() =5,
=5, ![]() 利用公式求回归系数
利用公式求回归系数![]() ,
,![]() ;(2)由(1)知回归方程为
;(2)由(1)知回归方程为![]() =1.23x+0.08,当x=10年时,
=1.23x+0.08,当x=10年时, ![]() =1.23×10+0.08=12.38(万元)。
=1.23×10+0.08=12.38(万元)。
试题解析:
(1)列表:
i | 1 | 2 | 3 | 4 | 5 |
xi | 2 | 3 | 4 | 5 | 6 |
yi | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
xiyi | 4.4 | 11.4 | 22.0 | 32.5 | 42.0 |
| 4 | 9 | 16 | 25 | 36 |
| |||||
于是![]() =
=![]() =1.23;
=1.23;
![]() =
=![]() -
-![]()
![]() =5-1.23×4=0.08.
=5-1.23×4=0.08.
(2)线性回归直线方程是![]() =1.23x+0.08,当x=10年时,
=1.23x+0.08,当x=10年时, ![]() =1.23×10+0.08=12.38(万元),即当使用10年时,估计支出总费用是12.38万元.
=1.23×10+0.08=12.38(万元),即当使用10年时,估计支出总费用是12.38万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点的零件的多少随机器的运转的速度的变化而变化,下表为抽样试验的结果:
转速
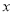 /(转/秒)
/(转/秒)16
14
12
8
每小时生产有缺点的零件数
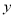 /件
/件11
9
8
5
(1)画出散点图;
(2)如果
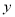 对
对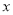 有线性相关关系,请画出一条直线近似地表示这种线性关系;
有线性相关关系,请画出一条直线近似地表示这种线性关系;(3)在实际生产中,若它们的近似方程为
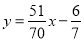 ,允许每小时生产的产品中有缺点的零件最多为
,允许每小时生产的产品中有缺点的零件最多为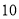 件,那么机器的运转速度应控制在什么范围内?
件,那么机器的运转速度应控制在什么范围内? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知
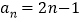 (
(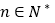 ).
).(Ⅰ)求证:
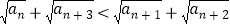 ;
;(Ⅱ)若不等式
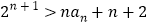 在
在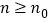 时恒成立,求最小正整数
时恒成立,求最小正整数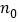 ,并给出证明.
,并给出证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=(λx+1)ln x-x+1.
(1)若λ=0,求f(x)的最大值;
(2)若曲线y=f(x)在点(1,f(1))处的切线与直线x+y+1=0垂直,证明:
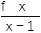 >0.
>0. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 与圆
与圆
 的公共点的轨迹为曲线
的公共点的轨迹为曲线 ,且曲线
,且曲线 与
与 轴的正半轴相交于点
轴的正半轴相交于点 .若曲线
.若曲线 上相异两点
上相异两点 满足直线
满足直线 的斜率之积为
的斜率之积为 .
.(1)求
 的方程;
的方程;(2)证明直线
 恒过定点,并求定点的坐标.
恒过定点,并求定点的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一个同学家开了一个小卖部,他为了研究气温对热饮销售的影响,经过统计,得到一个卖出的热饮杯数与当天气温的对比表:
摄氏温度/
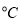
-5
0
4
7
12
15
19
23
27
31
36
热饮杯数
156
150
132
128
130
116
104
89
93
76
54
(1)画出散点图;
(2)从散点图中发现气温与热饮销售杯数之间关系的一般规律;
(3)求回归方程;
(4)如果某天的气温是
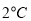 ,预测这天卖出的热饮杯数.
,预测这天卖出的热饮杯数. -
科目: 来源: 题型:
查看答案和解析>>【题目】【湖南省2017届高三长郡中学、衡阳八中等十三校重点中学第一次联考数学(理)】
已知函数
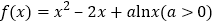 .
.(1)当
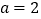 时,试求函数图像过点
时,试求函数图像过点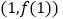 的切线方程;
的切线方程;(2)当
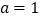 时,若关于
时,若关于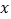 的方程
的方程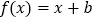 有唯一实数解,试求实数
有唯一实数解,试求实数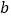 的取值范围;
的取值范围;(3)若函数
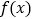 有两个极值点
有两个极值点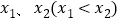 ,且不等式
,且不等式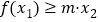 恒成立,试求实数
恒成立,试求实数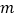 的取值范围.
的取值范围.
相关试题

