【题目】如图， 是圆的直径，点是圆上异于的点， 垂直于圆所在的平面，且．

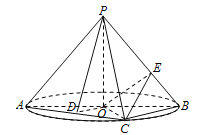
（1）若为线段的中点，求证平面；

（2）求三棱锥体积的最大值；

（3）若，点在线段上，求的最小值．

【答案】（1）见解析（2）（3）．

【解析】试题分析：

(1)由等腰三角形三线合一可得，由线面垂直的定义可得，最后利用线面垂直的判断定理可得平面．

(2)当底面ABC面积最大时，三棱锥体积由最大值，由几何关系可得当时， 面积的最大值为，结合三棱锥体积公式可得三棱锥体积的最大值为．

(3)将将侧面绕旋转至平面C，使之与平面共面，由平面几何的知识可知， ， 共线时， 取得最小值．结合筝形的性质计算可得的最小值为．

试题解析：

（1）在中，因为， 为的中点，所以．

又垂直于圆所在的平面，所以．

因为，所以平面．

（2）因为点在圆上，所以当时， 到的距离最大，且最大值为．

又，所以面积的最大值为．

又因为三棱锥的高，

故三棱锥体积的最大值为．

（3）在中， ， ，所以．

同理，所以．在三棱锥中，将侧面绕旋转至平面C，使之与平面共面，如图所示．

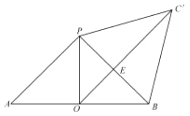
当， ， 共线时， 取得最小值．

又因为， ，所以垂直平分，即为中点．

从而，

亦即的最小值为．

关闭