搜索
设f（x）=3x-x2，则在下列区间中，使函数f（x）有零点的区间是
- A.[0，1]
- B.[1，2]
- C.[-2，-1]
- D.[-1，0]
D
分析：令f（x）=3x-x2=0，得3x=x2，分别作出函数y=3x，t=x2的图象
观察图象的交点所在区间即可．
解答：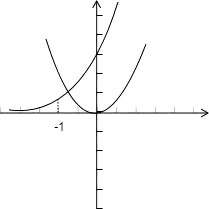
解：∵f（-1）=3-1-（-1）2=
-1=-
＜0，
f（0）=30-02=1＞0，
∴f（-1）•f（0）＜0，∴有零点的区间是[-1，0]．
【答案】D
点评：二分法是求方程根的一种基本算法，其理论依据是零点存在定理：一般地，若函数y=f（x）在区间[a，b]上的图象是一条不间断的曲线，且f（a）f（b）＜0，则函数y=f（x）在区间（a，b）上有零点．
分析：令f（x）=3x-x2=0，得3x=x2，分别作出函数y=3x，t=x2的图象
观察图象的交点所在区间即可．
解答：
解：∵f（-1）=3-1-（-1）2=-1=-＜0，f（0）=30-02=1＞0，
∴f（-1）•f（0）＜0，∴有零点的区间是[-1，0]．
【答案】D
点评：二分法是求方程根的一种基本算法，其理论依据是零点存在定理：一般地，若函数y=f（x）在区间[a，b]上的图象是一条不间断的曲线，且f（a）f（b）＜0，则函数y=f（x）在区间（a，b）上有零点．
