【题目】某企业欲做一个介绍企业发展史的铭牌,铭牌的截面形状是如图所示的扇形环面(由扇形![]() 挖去扇形
挖去扇形![]() 后构成的).已知
后构成的).已知![]() ,线段
,线段![]() 与弧
与弧![]() 、弧
、弧![]() 的长度之和为
的长度之和为![]() 米,圆心角为
米,圆心角为![]() 弧度.
弧度.

(1)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(2)记铭牌的截面面积为![]() ,试问
,试问![]() 取何值时,
取何值时,![]() 的值最大?并求出最大值.
的值最大?并求出最大值.
参考答案:
【答案】(1)![]() ;(2)当
;(2)当![]() 米时铭牌的面积最大,且最大面积为
米时铭牌的面积最大,且最大面积为![]() 平方米.
平方米.
【解析】试题分析:(1)更具体求出扇形的周长,即可得到![]() 关于
关于![]() 的函数解析式;;
的函数解析式;;
(2)根据扇形面积公式,求出函数解析式利用二次函数求出![]() 的值最大.
的值最大.
试题解析:(1)根据题意,可算得弧![]() (
(![]() ),弧
),弧![]() (
(![]() ).
).
又![]() ,
,
于是,![]() ,
,
所以,![]() .
.
(2) 依据题意,可知![]()
化简,得![]()
![]() .
.
于是,当![]() (满足条件
(满足条件![]() )时,
)时,![]() (
(![]() ).
).
答 所以当![]() 米时铭牌的面积最大,且最大面积为
米时铭牌的面积最大,且最大面积为![]() 平方米.
平方米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 .
.(1)当
 时,讨论函数
时,讨论函数 的单调性;
的单调性;(2)当
 时,对于任意正实数
时,对于任意正实数 ,不等式
,不等式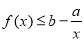 恒成立,试判断实数
恒成立,试判断实数 的大小关系.
的大小关系. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,曲线
中,曲线 的参数方程为
的参数方程为 (
( ,
,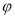 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,直线
轴正半轴为极轴建立极坐标系,直线 的极坐标方程为
的极坐标方程为 ,若直线
,若直线 与曲线
与曲线 相切;
相切; (1)求曲线
 的极坐标方程与直线
的极坐标方程与直线 的直角坐标方程;
的直角坐标方程;(2)在曲线
 上取两点
上取两点 ,
, 与原点
与原点 构成
构成 ,且满足
,且满足 ,求
,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知圆
 ,直线
,直线 ,在圆
,在圆 内任取一点
内任取一点 ,则
,则 到直线的距离大于2的概率为__________.
到直线的距离大于2的概率为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的定义域为
的定义域为 ;
;(1)求实数
 的取值范围;
的取值范围;(2)设实数
 为
为 的最大值,若实数
的最大值,若实数 ,
, ,
, 满足
满足 ,求
,求 的最小值.
的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义域为
 的函数
的函数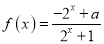 是奇函数
是奇函数(Ⅰ)求
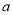 值;
值;(Ⅱ)判断并证明该函数在定义域
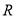 上的单调性;
上的单调性;(Ⅲ)若对任意的
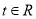 ,不等式
,不等式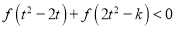 恒成立,求实数
恒成立,求实数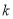 的取值范围;
的取值范围;(Ⅳ)设关于
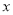 的函数
的函数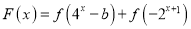 有零点,求实数
有零点,求实数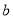 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知复数
 满足
满足 ,
, 的虚部为2,
的虚部为2,(1)求复数
 ;
;(2)设
 在复平面上对应点分别为
在复平面上对应点分别为 ,求
,求 的面积.
的面积.
相关试题

