【题目】已知函数![]() .
.
(Ⅰ)当![]() 时,求曲线
时,求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)若函数![]() 在
在![]() 上单调递减,试求
上单调递减,试求![]() 的取值范围;
的取值范围;
(Ⅲ)若函数![]() 的最小值为
的最小值为![]() ,试求
,试求![]() 的值.
的值.
参考答案:
【答案】(Ⅰ)![]() .(Ⅱ)
.(Ⅱ)![]() .(Ⅲ)
.(Ⅲ)![]() .
.
【解析】试题分析:(Ⅰ)利用导数求出![]() 处的切线斜率,根据点斜式写出切线方程;(Ⅱ)函数
处的切线斜率,根据点斜式写出切线方程;(Ⅱ)函数![]() 在
在![]() 上单调递减,即当
上单调递减,即当![]() 时,
时, ![]() 恒成立,等价于
恒成立,等价于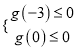 ,即可求出
,即可求出![]() 的取值范围;(Ⅲ)根据函数的单调性,得出函数
的取值范围;(Ⅲ)根据函数的单调性,得出函数![]() 的最小值只能在
的最小值只能在![]() 处取得,从而求得
处取得,从而求得![]() 的值.
的值.
试题解析:(Ⅰ)当![]() 时,由
时,由![]() 得:
得: ![]() .
.
又∵![]()
∴![]() .
.
∴切线方程为: ![]() ,即
,即![]() .
.
(Ⅱ)∵函数![]() 在
在![]() 上单调递减
上单调递减
∴当![]() 时,
时, ![]() 恒成立,即当
恒成立,即当![]() 时,
时, ![]() 恒成立.
恒成立.
∵函数![]() 的对称轴为
的对称轴为![]() ,并且开口向上,
,并且开口向上,
∴当![]() 时,函数
时,函数![]() 单调递减;当
单调递减;当![]() 时,函数
时,函数![]() 单调递增.
单调递增.
∴“当![]() 时,
时, ![]() 恒成立”必须满足:
恒成立”必须满足: 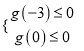 ,解得
,解得![]() .
.
∴![]() ,
, ![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)设![]() .
.
①当![]() 时,
时, ![]() ,
, ![]() 恒成立,
恒成立,
∴![]() 恒成立,
恒成立, ![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 没有最小值.
没有最小值.
②当![]() 时,
时, ![]() .
.
令![]() 得:
得: ![]() ,解得
,解得![]() .
.
∴当![]() 时,
时, ![]() ,
, ![]() 单调递增;
单调递增;
当![]() 时,
时, ![]() ,
, ![]() 单调递减;
单调递减;
当![]() 时,
时, ![]() ,
, ![]() 单调递增.
单调递增.
∴当![]() 时,
时, ![]() 取得极大值;
取得极大值;
当![]() 时,
时, ![]() 取得极小值.
取得极小值.
∴当![]() 时,
时, ![]() ,
,
∴![]() ,则
,则![]() ,
,
又∵函数![]() 的最小值为
的最小值为![]() ,
,
∴函数![]() 的最小值只能在
的最小值只能在![]() 处取得,则
处取得,则![]() ,
,
∴![]() ,即
,即![]() ,解得
,解得![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
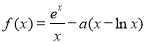 .
.(1)当
 时,试求
时,试求 在
在 处的切线方程;
处的切线方程;(2)当
 时,试求
时,试求 的单调区间;
的单调区间;(3)若
 在
在 内有极值,试求
内有极值,试求 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中,  ,
,  为边
为边 的中点,将
的中点,将 沿直线
沿直线 翻转成
翻转成 .若
.若 为线段
为线段 的中点,则在
的中点,则在 翻折过程中:
翻折过程中:
①
 是定值;②点
是定值;②点 在某个球面上运动;
在某个球面上运动;③存在某个位置,使
 ;④存在某个位置,使
;④存在某个位置,使 平面
平面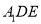 .
.其中正确的命题是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知四棱锥
 的底面为平行四边形,且
的底面为平行四边形,且 ,
, ,
,  分别为
分别为 中点,过
中点,过 作平面
作平面 分别与线段
分别与线段 相交于点
相交于点 .
.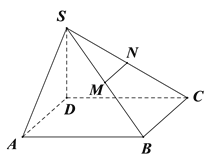
(Ⅰ)在图中作出平面
 使面
使面 ‖
‖ (不要求证明);
(不要求证明);(II)若
 ,在(Ⅰ)的条件下求多面体
,在(Ⅰ)的条件下求多面体 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,三棱台
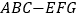 的底面是正三角形,平面
的底面是正三角形,平面 平面
平面 ,
, ,
, .
.
(Ⅰ)求证:
 ;
;(Ⅱ)若
 和梯形
和梯形 的面积都等于
的面积都等于 ,求三棱锥
,求三棱锥 的体积.
的体积. -
科目: 来源: 题型:
查看答案和解析>>【题目】一只小蜜蜂位于数轴上的原点处,小蜜蜂每一次具有只向左或只向右飞行一个单位或者两个单位距离的能力,且每次飞行至少一个单位.若小蜜蜂经过5次飞行后,停在数轴上实数3位于的点处,则小蜜蜂不同的飞行方式有多少种?( )
A. 5 B. 25 C. 55 D. 75
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB⊥AC,若AD⊥BC,则AB2=BD·BC;类似地有命题:在三棱锥A-BCD中,AD⊥平面ABC,若A点在平面BCD内的射影为M,则有S
 =S△BCM·S△BCD.上述命题是 ( )
=S△BCM·S△BCD.上述命题是 ( )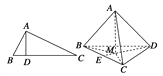
A. 真命题
B. 增加条件“AB⊥AC”才是真命题
C. 增加条件“M为△BCD的垂心”才是真命题
D. 增加条件“三棱锥A-BCD是正三棱锥”才是真命题
相关试题

