【题目】在每年的春节后，某市政府都会发动公务员参与到植树绿化活动中去．林业管理部门在植树前，为了保证树苗的质量，都会在植树前对树苗进行检测．现从甲、乙两种树苗中各抽测了10株树苗，量出它们的高度如下（单位：厘米）：

甲：37，21，31，20，29，19，32，23，25，33；

乙：10，30，47，27，46，14，26，10，44，46．

（1）画出两组数据的茎叶图，并根据茎叶图对甲、乙两种树苗的高度作比较，写出两个统计结论；

（2）设抽测的10株甲种树苗高度平均值为，将这10株树苗的高度依次输入，按程序框（如图）进行运算，问输出的S大小为多少？并说明S的统计学意义．

参考答案：

【答案】（1）详见解析（2），S越小表越整齐，相反参差不齐

【解析】试题分析：（1）画出茎叶图，通过图能判断甲，乙两种树苗的平均高度、分散情况、中位数的值；（2）直接利用均值与方差公式求解，说明几何意义即可

试题解析：（1）茎叶图；

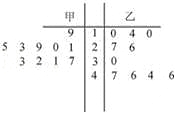
统计结论：

①甲种树苗的平均高度小于乙种树苗的平均高度；

②甲种树苗比乙种树苗长得整齐；

③甲种树苗的中位数为27，乙种树苗的中位数为28．5；

④甲种树苗的高度基本上是对称的，而且大多数集中在均值附近，乙种树苗的高度分布比较分散．

（2），

=35

S表示10株甲种树苗高度的方差．是描述树苗高度离散程度的量，S越小表越整齐，相反参差不齐．

关闭