【题目】已知函数![]() .
.
(1)求函数![]() 的最值;
的最值;
(2)函数![]() 图像在点
图像在点![]() 处的切线斜率为
处的切线斜率为![]() 有两个零点
有两个零点![]() ,求证:
,求证:![]() .
.
参考答案:
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)先求导数,得导函数零点,根据a的正负讨论导函数符号变化规律,确定单调性,进而确定最值取法,(2)先根据导数几何意义确定a的值,再根据零点条件列等量关系:![]() ,根据目标不等式构造
,根据目标不等式构造![]() ,最后利用导数研究函数
,最后利用导数研究函数![]() 最值可证不等式
最值可证不等式
试题解析:(1)![]() ,
,![]()
当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,有最小值
上单调递增,有最小值![]() ,无最大值;
,无最大值;
当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,有最大值
上单调递减,有最大值![]() ,无最小值.
,无最小值.
(2)依题知![]() ,即
,即![]() ,所以
,所以![]() ,
,![]() ,
,![]()
所以![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
因为![]() 是
是![]() 的两个零点,必然一个小于
的两个零点,必然一个小于![]() ,一个大于
,一个大于![]() ,不妨设
,不妨设![]() .
.
因为![]() ,
,![]()
所以![]() ,
,
变形为![]() .
.
欲证![]() ,只需证
,只需证![]() ,
,
即证![]() .
.
令![]() ,则只需证
,则只需证![]() 对任意的
对任意的![]() 都成立.
都成立.
令![]() ,则
,则![]()
所以![]() 在
在![]() 上单增,
上单增,![]()
即![]() 对任意的
对任意的![]() 都成立.
都成立.
所以![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线
 上的点
上的点 到点
到点 的距离与到直线
的距离与到直线 的距离之差为
的距离之差为 ,过点
,过点 的直线
的直线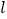 交抛物线于
交抛物线于 两点.
两点.(1)求抛物线的方程;
(2)若
 的面积为
的面积为 ,求直线
,求直线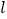 的方程.
的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】设a∈R,f(x)=
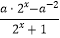 为奇函数.
为奇函数.
(1)求函数F(x)=f(x)+2x﹣ ﹣1的零点;
﹣1的零点;
(2)设g(x)=2log2( ),若不等式f﹣1(x)≤g(x)在区间[
),若不等式f﹣1(x)≤g(x)在区间[  ,
,  ]上恒成立,求实数k的取值范围.
]上恒成立,求实数k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有人说:“掷一枚骰子一次得到的点数是2的概率是
 ,这说明掷一枚骰子6次会出现一次点数是2.”对此说法,同学中出现了两种不同的看法:一些同学认为这种说法是正确的.他们的理由是:因为掷一枚骰子一次得到点数是2的概率是
,这说明掷一枚骰子6次会出现一次点数是2.”对此说法,同学中出现了两种不同的看法:一些同学认为这种说法是正确的.他们的理由是:因为掷一枚骰子一次得到点数是2的概率是 ,所以掷一枚骰子6次得到一次点数是2的概率P=
,所以掷一枚骰子6次得到一次点数是2的概率P= ×6=1,即“掷一枚骰子6次会出现一次点数是2”是必然事件,一定发生.还有一些同学觉得这种说法是错误的,但是他们却讲不出是什么理由来.你认为这种说法对吗?请说出你的理由.
×6=1,即“掷一枚骰子6次会出现一次点数是2”是必然事件,一定发生.还有一些同学觉得这种说法是错误的,但是他们却讲不出是什么理由来.你认为这种说法对吗?请说出你的理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】植树节某班20名同学在一段直线公路一侧植树,每人植一棵,相邻两棵树相距10米.开始时需将树苗集中放置在某一树坑旁边,使每位同学从各自树坑出发前来领取树苗往返所走的路程总和最小,这个最小值为 (米).
-
科目: 来源: 题型:
查看答案和解析>>【题目】家用电器一件,现价2000元,实行分期付款,每期付款数相同,每期为一月,购买后一个月付款一次,共付12次,即购买后一年付清,如果按月利率8‰,每月复利一次计算,那么每期应付款多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于利用斜二侧法得到的直观图有下列结论:①三角形的直观图是三角形;②平行四边形的直观图是平行四边形;③正方形的直观图是正方形;④菱形的直观图是菱形,以上结论正确的是( )
A. ①② B. ① C. ③④ D. ①②③④
相关试题

