(本小题满分14分)
已知数列![]() ,
,![]() ,其中
,其中![]() ,数列
,数列![]() 的前
的前![]() 项和
项和![]() ,数列
,数列![]() 满足
满足![]() ,
,![]() .
.
(Ⅰ)求数列![]() ,
,![]() 的通项公式;
的通项公式;
(Ⅱ)是否存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立?若存在,求出
恒成立?若存在,求出![]() 的最小值;
的最小值;
(Ⅲ)若数列![]() 满足
满足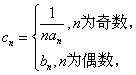 当
当![]() 是偶数时,求数列
是偶数时,求数列![]() 的前
的前![]() 项和
项和![]() .
.
(本小题满分14分)
解:(Ⅰ)因为![]() ,
,
当![]() 时,
时,![]() .
.
所以![]() .
.
所以![]() .
.
即![]() .
.
又![]() ,
,
所以![]()
![]()
![]() .……………………………………………………………………3分
.……………………………………………………………………3分
当![]() 时,上式成立
时,上式成立
因为![]() ,
,![]() ,
,
所以![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列,故
的等比数列,故![]() .…………………5分
.…………………5分
(Ⅱ)由(Ⅰ)知,![]() .
.
则![]() .…………………7分
.…………………7分
假设存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立,
恒成立,
即![]() 恒成立.
恒成立.
由![]() ,解得
,解得![]() .
.
所以存在自然数![]() ,使得对于任意
,使得对于任意![]() ,
,![]() ,有
,有![]() 恒成立.此时
恒成立.此时![]() 的最小值为
的最小值为![]() .……………………………………………………10分
.……………………………………………………10分
(Ⅲ)当![]() 是奇数时,
是奇数时,
![]()
![]()
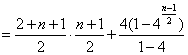
![]() .……………………………………………………12分
.……………………………………………………12分
当![]() 是偶数时,
是偶数时,
![]()
![]()
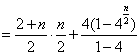
![]() .
.
因此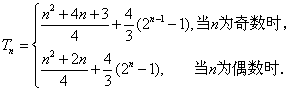 …………………………14分
…………………………14分

