定义在实数R上的函数y= f(x)是偶函数.当x≥0时..在R上的表达式,的最大值.并写出f(x)在R上的单调区间. 题目和参考答案 ——青夏教育精英家教网—

（本小题满分12分）定义在实数R上的函数y= f（x）是偶函数，当x≥0时，.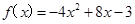
（Ⅰ）求f（x）在R上的表达式；
（Ⅱ）求y=f（x）的最大值，并写出f（x）在R上的单调区间（不必证明）.

（Ⅰ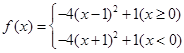）；（Ⅱ）最大值1，单调递增区间是（-∞，-1和[0，1] ，单调递减区间是 [-1，0]和[1，+∞。
单调递减区间是 [-1，0]和[1，+∞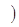

解析试题分析：解：（Ⅰ）设x＜0，则- x＞0，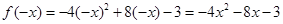
∵f（x）是偶函数，∴f（-x）=f（x）         …………… 3
∴x＜0时，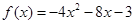
所以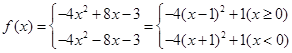  ……………6
（Ⅱ）y=f（x）开口向下，所以y=f（x）有最大值f（1）=f（-1）=1
函数y=f（x）的单调递增区间是（-∞，-1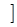和[0，1]       …………… 9
单调递减区间是 [-1，0]和[1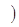，+∞       ……………12
考点：函数的奇偶性；函数的最值；函数的单调性；函数解析式的求法。
点评：利用函数的奇偶性求函数的解析式，这类问题的一般做法是： ①“求谁设谁”即求哪个区间上的解析式，x就设在哪个区间内； ②要利用已知区间的解析式进行代入； ③利用f(x)的奇偶性写出-f(x)或f(-x)从而解出f(x)。