【题目】如图,在四棱台![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,
,![]() ,
,![]() 平面
平面![]() .
.

(1)若点![]() 是
是![]() 的中点,求证:
的中点,求证:![]() //平面
//平面![]() ;
;
(2)棱BC上是否存在一点E,使得二面角![]() 的余弦值为
的余弦值为![]() ?若存在,求线段CE的长;若不存在,请说明理由.
?若存在,求线段CE的长;若不存在,请说明理由.
参考答案:
【答案】(1)详见解析;(2)存在,且长度为![]()
【解析】
(1) 连接![]() ,可得四边形
,可得四边形![]() 是平行四边形,可得
是平行四边形,可得![]() ,可证得
,可证得![]() //平面
//平面![]() ;
;
(2)取![]() 中点
中点![]() ,连接
,连接![]() ,可得
,可得![]() 是正三角形,分别以
是正三角形,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,假设点
轴,建立空间直角坐标系,假设点![]() 存在,设点
存在,设点![]() 的坐标为
的坐标为![]() ,
,![]() ,可得平面
,可得平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量为
的一个法向量为![]() ,由二面角
,由二面角![]() 的余弦值为
的余弦值为![]() 可得
可得![]() 的值,可得
的值,可得![]() 的长.
的长.
解:(1)证明:连接![]() ,由已知得,
,由已知得,![]() ,且
,且![]()
所以四边形![]() 是平行四边形,即
是平行四边形,即![]() ,
,

又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]()
(2)取![]() 中点
中点![]() ,连接
,连接![]() 因为
因为![]() 是菱形,且
是菱形,且![]() ,所以
,所以![]() 是正三角形,
是正三角形,
所以![]() 即
即![]() ,
,
由于![]() 是正三角形
是正三角形
所以,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴,建立空间直角坐标系,如图
轴,建立空间直角坐标系,如图![]() ,
,
![]() ,
,![]() ,
,![]()
假设点![]() 存在,设点
存在,设点![]() 的坐标为
的坐标为![]() ,
,![]()
![]() ,
,![]()
设平面![]() 的法向量
的法向量![]()
则 即
即![]() ,可取
,可取![]()
平面![]() 的法向量为
的法向量为![]()
所以,![]() ,解得:
,解得:![]()
又由于二面角![]() 大小为锐角,由图可知,点E在线段QC上,
大小为锐角,由图可知,点E在线段QC上,
所以![]() ,即
,即![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛掷一个质地均匀的骰子的试验,事件A表示“小于5的偶数点出现”,事件B表示“不小于5的点数出现”,则一次试验中,事件A或事件B至少有一个发生的概率为( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2017年11月、12月全国大范围流感爆发,为研究昼夜温差大小与患感冒人数多少之间的关系,一兴趣小组抄录了某医院11月到12月间的连续6个星期的昼夜温差情况与因患感冒而就诊的人数,得到如下资料:
日期
第一周
第二周
第三周
第四周
第五周
第六周
昼夜温差x(°C)
10
11
13
12
8
6
就诊人数y(个)
22
25
29
26
16
12
该兴趣小组确定的研究方案是:先从这六组数据中选取2组,用剩下的4组数据求线性回归方程,再用被选取的2组数据进行检验。
(Ⅰ)求选取的2组数据恰好是相邻两个星期的概率;
(Ⅱ)若选取的是第一周与第六周的两组数据,请根据第二周到第五周的4组数据,求出
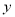 关于
关于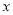 的线性回归方程
的线性回归方程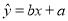 ;
;(Ⅲ)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2人,则认为得到的线性回归方程是理想的,试问该小组所得线性回归方程是否理想?
(参考公式:
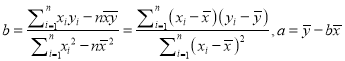 )
)参考数据:
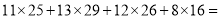 1092,
1092, 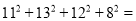 498
498 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知动圆过定点
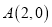 ,且在
,且在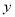 轴上截得弦
轴上截得弦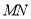 的长为4。
的长为4。(1)求动圆圆心的轨迹
 的方程;
的方程;(2)设
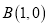 ,过点
,过点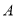 斜率为
斜率为 的直线
的直线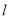 交轨迹
交轨迹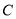 于
于 两点,
两点, 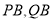 的延长线交轨迹
的延长线交轨迹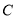 于
于 两点。
两点。①若
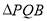 的面积为3,求
的面积为3,求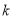 的值。
的值。②记直线
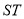 的斜率为
的斜率为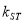 ,证明:
,证明: 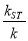 为定值,并求出这个定值。
为定值,并求出这个定值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
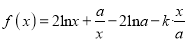 。
。(1)若
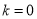 ,试判断
,试判断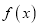 的零点的个数。
的零点的个数。(2)若
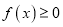 恒成立,求
恒成立,求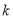 的取值范围。
的取值范围。 -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4-4:坐标系与参数方程]
在直角坐标系
 中,过点
中,过点 的直线
的直线 的参数方程为
的参数方程为 (
( 为参数).以原点
为参数).以原点 为极点,
为极点,  轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线 的极坐标方程为
的极坐标方程为 .
.(1)求直线
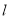 的普通方程和曲线
的普通方程和曲线 的直角坐标方程;
的直角坐标方程;(2)若直线
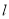 与曲线
与曲线 相交于
相交于 ,
,  两点,求
两点,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解户籍、性别对生育二胎选择倾向的影响,某地从育龄人群中随机抽取了容量为
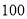 的调查样本,其中城镇户籍与农村户籍各
的调查样本,其中城镇户籍与农村户籍各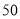 人;男性
人;男性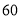 人,女性
人,女性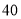 人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )
人,绘制不同群体中倾向选择生育二胎与倾向选择不生育二胎的人数比例图(如图所示),其中阴影部分表示倾向选择生育二胎的对应比例,则下列叙述中错误的是( )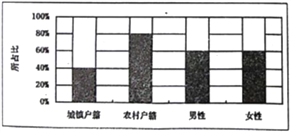
A. 是否倾向选择生育二胎与户籍有关
B. 是否倾向选择生育二胎与性别有关
C. 倾向选择生育二胎的人员中,男性人数与女性人数相同
D. 倾向选择不生育二胎的人员中,农村户籍人数少于城镇户籍人数
相关试题

