
【题目】某企业质量检验员为了检测生产线上零件的情况,从生产线上随机抽取了![]() 个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
个零件进行测量,根据所测量的零件尺寸(单位:mm),得到如下的频率分布直方图:
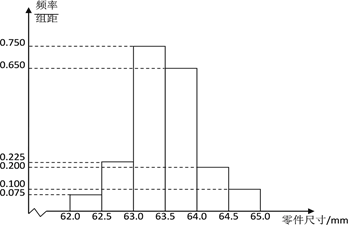
(1)根据频率分布直方图,求这![]() 个零件尺寸的中位数(结果精确到
个零件尺寸的中位数(结果精确到![]() );
);
(2)已知尺寸在![]() 上的零件为一等品,否则为二等品. 将这
上的零件为一等品,否则为二等品. 将这![]() 个零件尺寸的样本频率视为概率,从生产线上随机抽取
个零件尺寸的样本频率视为概率,从生产线上随机抽取![]() 个零件,试估计所抽取的零件是二等品的概率.
个零件,试估计所抽取的零件是二等品的概率.
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】已知关于x的一元二次不等式ax2+x+b>0的解集为(-∞,-2)∪(1,+∞).
(Ⅰ)求a和b的值;
(Ⅱ)求不等式ax2-(c+b)x+bc<0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )的离心率为
)的离心率为![]() ,左、右焦点分别为
,左、右焦点分别为![]() 、
、![]() ,
,![]() 为椭圆的下顶点,
为椭圆的下顶点,![]() 交椭圆于另一点
交椭圆于另一点![]() 、
、![]() 的面积
的面积![]() .
.
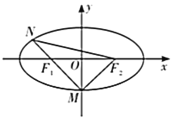
(1)求椭圆的方程;
(2)过点![]() 作直线
作直线![]() 交椭圆于
交椭圆于![]() 、
、![]() 两点,点
两点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,问:直线
,问:直线![]() 是否过定点?若是,请求出定点的坐标;若不是,请说明理由.
是否过定点?若是,请求出定点的坐标;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市约有20万住户,为了节约能源,拟出台“阶梯电价”制度,即制定住户月用电量的临界值![]() ,若某住户某月用电量不超过
,若某住户某月用电量不超过![]() 度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过
度,则按平价(即原价)0.5(单位:元/度)计费;若某月用电量超过![]() 度,则超出部分按议价
度,则超出部分按议价![]() (单位:元/度)计费,未超出部分按平价计费.为确定
(单位:元/度)计费,未超出部分按平价计费.为确定![]() 的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
的值,随机调查了该市100户的月用电量,统计分析后得到如图所示的频率分布直方图.根据频率分布直方图解答以下问题(同一组数据用该区间的中点值作代表).
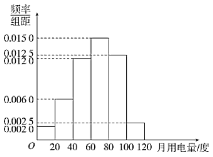
(1)若该市计划让全市70%的住户在“阶梯电价”出台前后缴纳的电费不变,求临界值![]() ;
;
(2)在(1)的条件下,假定出台“阶梯电价”之后,月用电量未达![]() 度的住户用电量保持不变;月用电量超过
度的住户用电量保持不变;月用电量超过![]() 度的住户节省“超出部分”的60%,试估计全市每月节约的电量.
度的住户节省“超出部分”的60%,试估计全市每月节约的电量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 是抛物线
是抛物线![]() 的顶点,
的顶点,![]() ,
,![]() 是
是![]() 上的两个动点,且
上的两个动点,且![]() .
.
(1)判断点![]() 是否在直线
是否在直线![]() 上?说明理由;
上?说明理由;
(2)设点![]() 是△
是△![]() 的外接圆的圆心,点
的外接圆的圆心,点![]() 到
到![]() 轴的距离为
轴的距离为![]() ,点
,点![]() ,求
,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的长轴长为4,离心率为
的长轴长为4,离心率为![]() .直线
.直线![]() 交于点
交于点![]() ,倾斜角互补,且直线
,倾斜角互补,且直线![]() 与椭圆
与椭圆![]() 的交点分别为
的交点分别为![]() (点
(点![]() 在点
在点![]() 的右侧).
的右侧).
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)证明:直线![]() 的斜率为定值;
的斜率为定值;
(Ⅲ)在椭圆上是否存在一点![]() ,恰好使得四边形
,恰好使得四边形![]() 为平行四边形,若存在,分别指出此时点
为平行四边形,若存在,分别指出此时点![]() 和
和![]() 的坐标;若不存在,简述理由.
的坐标;若不存在,简述理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,原点到直线
,原点到直线![]() 的距离为
的距离为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知定点![]() ,是否存在过
,是否存在过![]() 的直线
的直线![]() ,使
,使![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两点,且以
两点,且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的左顶点?若存在,求出
的左顶点?若存在,求出![]() 的方程:若不存在,请说明理由.
的方程:若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com