【题目】选修4-4:坐标系与参数方程
在直角坐标系![]() 中,直线
中,直线![]() 的方程为
的方程为![]() ,曲线
,曲线![]() :
:![]() (
(![]() 为参数,
为参数,![]() ),在以原点
),在以原点![]() 为极点,
为极点,![]() 轴正半轴为极轴的极坐标系中,曲线
轴正半轴为极轴的极坐标系中,曲线![]() :
:![]() .
.
(1)求曲线![]() 的普通方程和曲线
的普通方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)若直线![]() 与曲线
与曲线![]() 有公共点,且直线
有公共点,且直线![]() 与曲线
与曲线![]() 的交点
的交点![]() 恰好在曲线
恰好在曲线![]() 与
与![]() 轴围成的区域(不含边界)内,求
轴围成的区域(不含边界)内,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)消去参数,即可得到曲线![]() 的普通方程,根据极坐标与直角坐标的互化公式,即可化简得到曲线
的普通方程,根据极坐标与直角坐标的互化公式,即可化简得到曲线![]() 的直角坐标方程.
的直角坐标方程.
(2)根据直线![]() 与曲线
与曲线![]() 有公共点,解得
有公共点,解得![]() ,再联立方程组
,再联立方程组![]() ,求得点
,求得点![]() 的坐标,根据点
的坐标,根据点![]() 在曲线
在曲线![]() 内,列出不等式组,即可求解。
内,列出不等式组,即可求解。
(1)曲线![]() 的普通方程为
的普通方程为![]() ,
,
曲线![]() 的直角坐标方程为
的直角坐标方程为![]() .
.
(2)直线![]() 与曲线
与曲线![]() 有公共点,则圆心
有公共点,则圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
故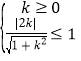 ,解得
,解得![]() .
.
由![]() ,得
,得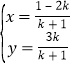 ,即
,即![]() ,
,
又点![]() 在曲线
在曲线![]() 内,所以
内,所以 ,解得
,解得![]() .
.
综上,![]() 的取值范围为
的取值范围为![]() .
.

