Question

【题目】已知函数的部分图象如图所示：

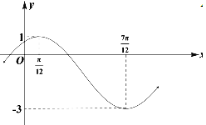
（1）求的解析式；

（2）求的单调区间和对称中心坐标；

（3）将的图象向左平移个单位，再将横坐标伸长到原来的2倍，纵坐标不变，最后将图象向上平移1个单位，得到函数的图象，求函数在上的最大值和最小值．

Answer 1

【答案】（1）；（2）的单调递增区间为，，单调递减区间为，；对称中心的坐标为，；（3）最大值，最小值-2.

【解析】

（1）由图象可求，的值，求得周期，利用周期公式可求，由可求，即可得解的解析式；

（2）令，，得，，可求的单调递增区间，令，，得，，可求的对称中心的坐标；

（3）由已知的图象变换过程可得：，由，利用正弦函数的性质可求在上的最大值和最小值．

（1）由图象可知，

解得，

又由于，

所以，

由，

，

又，

所以，

所以；

（2）由（1）知，，

令，，

得，，

所以的单调递增区间为，，

令，，

得，，

所以的单调递减区间为，，

令，，得，，

所以的对称中心的坐标为，；

（3）由已知的图象变换过程可得：，

因为，

所以，

所以当，得时，取得最小值，

当时，即时，取得最大值．