【题目】已知抛物线C:y2=4x的焦点为F,过点F的直线l与C相交于A,B两点,若|AB|=8,求直线l的方程.
参考答案:
【答案】![]()
【解析】试题分析:设直线l的方程为:y=k(x-1),代入y2=4x,整理得k2x2-(2k2+4)x+k2=0,利用韦达定理和抛物线的定义,能够求出直线l的方程.
试题解析:
抛物线y2=4x的焦点为F(1,0),当直线l斜率不存在时,|AB|=4,不合题意.设直线l的方程为y=k(x-1),代入y2=4x,整理得k2x2-(2k2+4)x+k2=0.
设A(x1,y1),B(x2,y2),由题意知k≠0,
则x1+x2=![]() .
.
由抛物线定义知,
|AB|=|AF|+|BF|=x1+1+x2+1=x1+x2+2,
∴x1+x2+2=8,即![]() +2=8.
+2=8.
解得k=±1.
所以直线l的方程为y=±(x-1),
即x-y-1=0,x+y-1=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据要求求值:
(1)用辗转相除法求123和48的最大公约数.
(2)用更相减损术求80和36的最大公约数.
(3)把89化为二进制数. -
科目: 来源: 题型:
查看答案和解析>>【题目】在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)求函数
 的单调区间;
的单调区间;(2)若
 ,证明:对任意的实数
,证明:对任意的实数 ,都有
,都有 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】小明计划在8月11日至8月20日期间游览某主题公园.根据旅游局统计数据,该主题公园在此期间“游览舒适度”(即在园人数与景区主管部门核定的最大瞬时容量之比,40%以下为舒适,40%—60%为一般,60%以上为拥挤)情况如图所示.小明随机选择8月11日至8月19日中的某一天到达该主题公园,并游览2天.
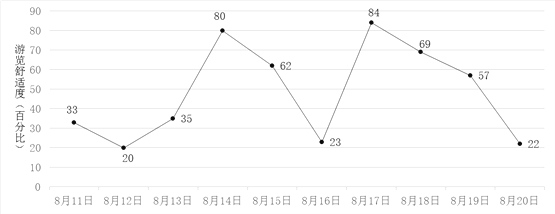 (Ⅰ)求小明连续两天都遇上拥挤的概率;
(Ⅰ)求小明连续两天都遇上拥挤的概率;(Ⅱ)设
 是小明游览期间遇上舒适的天数,求
是小明游览期间遇上舒适的天数,求 的分布列和数学期望;
的分布列和数学期望;(Ⅲ)由图判断从哪天开始连续三天游览舒适度的方差最大?(结论不要求证明)
-
科目: 来源: 题型:
查看答案和解析>>【题目】从甲、乙两名学生中选拔一人参加射箭比赛,为此需要对他们的射箭水平进行测试.现这两名学生在相同条件下各射箭10次,命中的环数如表:
甲
8
9
7
9
7
6
10
10
8
6
乙
10
9
8
6
8
7
9
7
8
8
(1)计算甲、乙两人射箭命中环数的平均数和标准差;
(2)比较两个人的成绩,然后决定选择哪名学生参加射箭比赛. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解某地高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
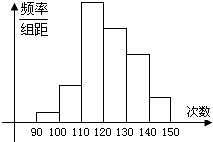
(1)第二小组的频率是多少?样本容量是多少?
(2)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
(3)通过该统计图,可以估计该地学生跳绳次数的众数是 , 中位数是 .
相关试题

