【题目】“中国剩余定理”又称“孙子定理”．1852年，英国来华传教士伟烈亚力将《孙子算经》中“物不知数”问题的解法传至欧洲．1874年，英国数学家马西森指出此法符合1801年由高斯得到的关于同余式解法的一般性定理，因而西方称之为“中国剩余定理”．“中国剩余定理”讲的是一个关于整除的问题，现有这样一个整除问题：将1到2019这2019个数中，能被3除余2且被5整除余2的数按从小到大的顺序排成一列，构成数列
，则此数列所有项中，中间项的值为（ ）
A.992B.1022C.1007D.1037
科目：高中数学 来源： 题型：
【题目】2014年，中央和国务院办公厅印发《关于引导农村土地经营权有序流转发展农业适度规模经营的意见》，要求大力发展土地流转和适度规模经营.某种粮大户2015年开始承包了一地区的大规模水田种植水稻，购买了一种水稻收割机若干台，这种水稻收割机随着使用年限的增加，每年的养护费也相应增加，这批水稻收割机自购买使用之日起，5年以来平均每台水稻收割机的养护费用数据统计如下：
年份 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代码 | 1 | 2 | 3 | 4 | 5 |
养护费用 | 1.1 | 1.6 | 2 | 2.5 | 2.8 |
（1）从这5年中随机抽取2年，求平均每台水稻收割机每年的养护费用至少有1年多于2万元的概率；
（2）求
关于
的线性回归方程；
（3）若该水稻收割机的购买价格是每台16万元，由(2)中的回归方程，从每台水稻收割机的年平均费用角度，你认为一台该水稻收割机是使用满5年就淘汰，还是继续使用到满8年再淘汰？
附：回归直线的斜率和截距的最小二乘法估计公式分别为：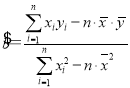
，
.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】体温是人体健康状况的直接反应，一般认为成年人腋下温度
（单位：
）平均在
之间即为正常体温，超过
即为发热.发热状态下，不同体温可分成以下三种发热类型：低热：
；高热：
；超高热（有生命危险）：
.
某位患者因患肺炎发热，于12日至26日住院治疗. 医生根据病情变化，从14日开始，以3天为一个疗程，分别用三种不同的抗生素为该患者进行消炎退热. 住院期间，患者每天上午8:00服药，护士每天下午16:00为患者测量腋下体温记录如下：
（1）请你计算住院期间该患者体温不低于
的各天体温平均值；
（2）在
日—
日期间，医生会随机选取
天在测量体温的同时为该患者进行某一特殊项目“
项目”的检查，记
为高热体温下做“项目”检查的天数，试求的分布列与数学期望；
（3）抗生素治疗一般在服药后2-8个小时就能出现血液浓度的高峰，开始杀灭细菌，达到消炎退热效果.假设三种抗生素治疗效果相互独立，请依据表中数据，判断哪种抗生素治疗效果最佳，并说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在平面直角坐标系
中，已知圆
过定点
，且在
轴上截得的弦长
，设动圆圆心的轨迹为曲线
．
（1）求曲线的方程；
（2）过点
作直线交曲线于
两点，问在曲线上是否存在一点
，使得点在以
为直径的圆上？若存在，求出点的坐标；若不存在，请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】马林●梅森是17世纪法国著名的数学家和修道士，也是当时欧洲科学界一位独特的中心人物，梅森在欧几里得、费马等人研究的基础上对2p﹣1作了大量的计算、验证工作，人们为了纪念梅森在数论方面的这一贡献，将形如2P﹣1（其中p是素数）的素数，称为梅森素数.若执行如图所示的程序框图，则输出的梅森素数的个数是（ ）
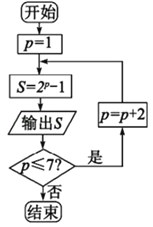
A.3B.4C.5D.6
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，在四棱锥
中，底面
为直角梯形，
，
，平面
平面，
为
的中点，
，
，
.
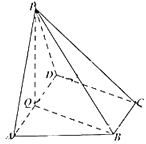
（1）求证：平面
平面
；
（2）若异面直线
与
所成角为
，求
的长；
（3）在（2）的条件下，求平面
与平面
所成锐二面角的余弦值.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，点
为圆
：
上一动点，过点分别作
轴，
轴的垂线，垂足分别为
，
，连接
延长至点
，使得
，点的轨迹记为曲线
.
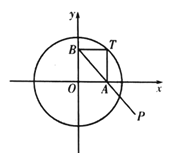
（1）求曲线的方程；
（2）若点，分别位于轴与轴的正半轴上，直线
与曲线相交于
，
两点，且
，试问在曲线上是否存在点
，使得四边形
为平行四边形，若存在，求出直线
方程；若不存在，说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
