【题目】已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,点
两点,点![]() 为抛物线
为抛物线![]() 的焦点且
的焦点且![]() .
.
(1)求![]() 的值;
的值;
(2)过点![]() 作不垂直于
作不垂直于![]() 轴的直线
轴的直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,问:在
两点,问:在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 轴总是平分
轴总是平分![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)存在;点
;(2)存在;点![]() .
.
【解析】
(1)联立![]() 和
和![]() ,设
,设![]() ,
,![]() ,根据韦达定理得到两根之和与两根之积,表示出
,根据韦达定理得到两根之和与两根之积,表示出![]() ,代入
,代入![]() 可解.
可解.
(2)先讨论直线![]() 斜率不存在的情况,此时显然存在这样的点;直线
斜率不存在的情况,此时显然存在这样的点;直线![]() 斜率存在时,设出直线方程,联立抛物线方程,由韦达定理表示
斜率存在时,设出直线方程,联立抛物线方程,由韦达定理表示![]() ,
,![]() 两点的坐标,再由
两点的坐标,再由![]() 轴总是平分
轴总是平分![]() ,得到
,得到![]() ,表示出
,表示出![]() 代入上式即可求解.
代入上式即可求解.
解:(1)根据条件可得点![]() 的坐标为
的坐标为![]() .
.
由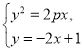 可得
可得![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
根据点![]() ,
,![]() 在抛物线上可得
在抛物线上可得![]() .
.
则![]() ,
,
∴![]() .
.
(2)由(1)可知抛物线![]() 的方程为
的方程为![]() .
.
当直线![]() 的斜率不存在时,
的斜率不存在时,![]() 轴上的除
轴上的除![]() 外的任一点均满足使
外的任一点均满足使![]() 轴平分
轴平分![]() .
.
当斜率存在时,由题可设直线![]() 的方程为
的方程为![]() ,
,![]() ,
,![]() .
.
联立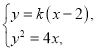 消去
消去![]() 得
得![]() ,
,
∴![]() ,
,![]() .
.
假设在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 轴平分
轴平分![]() ,则
,则![]() ,
,
∴![]() ,∴
,∴![]() .
.
又![]() ,
,![]() ,∴
,∴![]() .
.
把(*)式代入上式化简得![]() ,∴
,∴![]() ,
,
∴点![]() .
.
综上可知,在![]() 轴上存在一点
轴上存在一点![]() ,使得
,使得![]() 轴总是平分
轴总是平分![]() .
.

