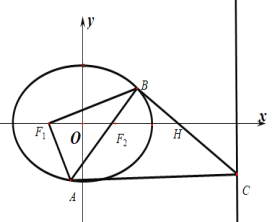
【题目】椭圆的焦点为和，过的直线交于两点，过作与轴垂直的直线，又知点，直线记为，与交于点．设，已知当时，．

（Ⅰ）求椭圆的方程；

（Ⅱ）求证：无论如何变化，点的横坐标是定值，并求出这个定值．

【答案】（Ⅰ）；（Ⅱ）定值为3

【解析】

（Ⅰ）设椭圆的方程为，当时，不妨设，则，由椭圆的定义得，从而，可得点A在y轴上，不妨设，由可得，将B代入椭圆方程即可；

（Ⅱ）设直线AB的方程为，，联立椭圆方程可得，进一步可得，，利用点斜式可得BH的方程以及直线的方程，解方程组即可.

（Ⅰ）设椭圆的方程为，其中，由已知，当时，不妨设，

则，又，所以，由椭圆的定义得，

从而，此时点A在y轴上，不妨设，

从而由已知条件可得，解得，

故，代入椭圆方程，解得，所以，

故所求椭圆方程为.

（Ⅱ）设直线AB的方程为，，将代入椭圆

中，得，即，

，所以，

由已知，，直线BH的斜率，

所以直线BH的方程为，而直线的方程为，代入，

解得，故点的横坐标是定值3.

关闭