搜索
【题目】已知椭圆C：
（
）经过
，
两点.O为坐标原点，且
的面积为
.过点
且斜率为k（
）的直线l与椭圆C有两个不同的交点M，N，且直线
，
分别与y轴交于点S，T.
（Ⅰ）求椭圆C的方程；
（Ⅱ）求直线l的斜率k的取值范围；
（Ⅲ）设
，
，求
的取值范围.
【答案】（Ⅰ）
（Ⅱ）
（Ⅲ）
【解析】
（Ⅰ）把点A坐标代入椭圆的方程得
.由
的面积为
可知，
，解得b，进而得椭圆C的方程.
（Ⅱ）设直线l的方程为
，
，
.联立直线l与椭圆C的方程可得关于x的一元二次方程.
，进而解得k的取值范围.
（Ⅲ）因为
，
，，，写出直线
的方程，令
，解得
.点S的坐标为
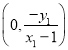.同理可得：点T的坐标为
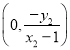.用坐标表示
，
，
，代入
，
，得
.同理
.由（Ⅱ）得
，
，代入
，化简再求取值范围.
（Ⅰ）因为椭圆C：
经过点，
所以
解得.
由的面积为可知，，
解得
，
所以椭圆C的方程为.
（Ⅱ）设直线l的方程为，，.
联立
，消y整理可得：
.
因为直线与椭圆有两个不同的交点，
所以
，解得
.
因为
，所以k的取值范围是.
（Ⅲ）因为，，，.
所以直线的方程是：
.
令，解得.
所以点S的坐标为.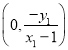
同理可得：点T的坐标为.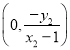
所以
，
，
.
由，，
可得：
，
，
所以.
同理.
由（Ⅱ）得，，
所以
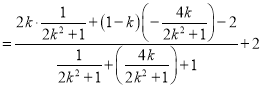
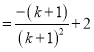
所以的范围是.
