【题目】若函数f(x)在区间A上,对a,b,c∈A,f(a),f(b),f(c)为一个三角形的三边长,则称函数f(x)为“三角形函数”.已知函数f(x)=xlnx+m在区间[ ![]() ,e]上是“三角形函数”,则实数m的取值范围为( )
,e]上是“三角形函数”,则实数m的取值范围为( )
A.![]()
B.![]()
C.![]()
D.![]()
参考答案:
【答案】A
【解析】解:若f(x)为“区域D上的三角形函数”.
则在区间D上,函数的最大值M和最小值m应满足:M>2m,
∵函数f(x)=xlnx+m在区间[ ![]() ,e]上是“三角形函数”,
,e]上是“三角形函数”,
f′(x)=lnx+1,
当x∈[ ![]() ,
, ![]() )时,f′(x)<0,函数f(x)递减;
)时,f′(x)<0,函数f(x)递减;
当x∈( ![]() ,e]时,f′(x)>0,函数f(x)递增;
,e]时,f′(x)>0,函数f(x)递增;
故当x= ![]() 时,函数f(x)取最小值﹣
时,函数f(x)取最小值﹣ ![]() +m,
+m,
又由f(e)=e+m,f( ![]() )=﹣
)=﹣ ![]() +m,
+m,
故当x=e时,函数f(x)取最大值e+m,
∴e+m>2(﹣ ![]() +m)>0,
+m)>0,
解得:m∈ ![]() ,
,
故选:A.
【考点精析】本题主要考查了函数的最值及其几何意义和函数的值的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值;函数值的求法:①配方法(二次或四次);②“判别式法”;③反函数法;④换元法;⑤不等式法;⑥函数的单调性法才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三棱锥ABCD的棱长都相等,E是AB的中点,则异面直线CE与BD所成角的余弦值为( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设关于
 的一元二次方程
的一元二次方程 .
.(1)若
 是从0,1,2,3,4五个数中任取的一个数,
是从0,1,2,3,4五个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率;(2)若
 是从区间
是从区间 上任取的一个数,
上任取的一个数, 是从区间
是从区间 上任取的一个数,求上述方程有实根的概率.
上任取的一个数,求上述方程有实根的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=lnx﹣
 ax2﹣bx,若x=1是f(x)的极大值点,则a的取值范围为( )
ax2﹣bx,若x=1是f(x)的极大值点,则a的取值范围为( )
A.(﹣1,0)
B.(﹣1,+∞)
C.(0,+∞)
D.(﹣∞,﹣1)∪(0,+∞) -
科目: 来源: 题型:
查看答案和解析>>【题目】已知a,b为正实数,函数f(x)=ax3+bx+2x在[0,1]上的最大值为4,则f(x)在[﹣1,0]上的最小值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有25周岁以上(含25周岁)工人300名,25周岁以下工人200名.为了研究工人的日平均生产量是否与年龄有关,现采用分层抽样的方法,从中抽取了100名工人,先统计了他们某月的日平均生产件数,然后按工人年龄在“25周岁以上(含25周岁)”和“25周岁以下”分为两组,再将两组工人的日平均生产件数分成5组:
 ,
, ,
, ,
,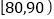 ,
, ,分别加以统计,得到如图所示的频率分布直方图.
,分别加以统计,得到如图所示的频率分布直方图.
(1)根据“25周岁以上组”的频率分布直方图,求25周岁以上组工人日平均生产件数的中位数的估计值(四舍五入保留整数);
(2)从样本中日平均生产件数不足60件的工人中随机抽取2人,求至多抽到一名“25周岁以下组”工人的概率。
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国是世界上严重缺水的国家,某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
 (吨),一位居民的月用水量不超过
(吨),一位居民的月用水量不超过 的部分按平价收费,超出
的部分按平价收费,超出 的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费。为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照 ,
, …,
…, 分成9组,制成了如图所示的频率分布直方图。
分成9组,制成了如图所示的频率分布直方图。
(1)求直方图中
 的值;
的值;(2)设该市有60万居民,估计全市居民中月均用水量不低于3吨的人数,并说明理由;
(3)若该市政府希望使82%的居民每月的用水量不超过标准
 (吨),估计
(吨),估计 的值,并说明理由。
的值,并说明理由。
相关试题

