【题目】南北朝时期的伟大数学家祖暅在数学上有突出贡献，他在实践的基础上提出祖暅原理：“幂势既同，则积不容异”.其含义是：夹在两个平行平面之间的两个几何体，被平行于这两个平行平面的任意平面所截，如果截得两个截面的面积总相等，那么这两个几何体的体积相等.如图，夹在两个平行平面之间的两个几何体的体积分别为
、
，被平行于这两个平面的任意平面截得的两个截面面积分别为
、
，则命题
：“、相等”是命题
“、总相等”的（ ）
A.充分不必要条件B.必要不充分条件
C.充要条件D.既不充分也不必要条件
科目：高中数学 来源： 题型：
【题目】有5名同学进行投篮比赛，决出第1名至第5名的不同名次，教练在公布成绩前透露，五名同学中的甲乙名次相邻，丙不是第一名，丁不是最后一名，根据教练的说法，这5名同学的名次排列最多有（ ）种不同的情况.
A.28B.32C.54D.64
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】太极图被称为“中华第一图”，闪烁着中华文明进程的光辉，它是由黑白两个鱼形纹组成的图案，俗称阴阳鱼，太极图展现了一种相互转化，相对统一的和谐美.定义：能够将圆O的周长和面积同时等分成两个部分的函数称为圆O的一个“太极函数”，设圆O：
，则下列说法中正确的是( )
A.函数
是圆O的一个太极函数
B.圆O的所有非常数函数的太极函数都不能为偶函数
C.函数
是圆O的一个太极函数
D.函数
的图象关于原点对称是为圆O的太极函数的充要条件
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】关于
的说法，正确的是（ ）
A.展开式中的二项式系数之和为1024B.展开式中第6项的二项式系数最大
C.展开式中第5项和第7项的二项式系数最大D.展开式中第6项的系数最小
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
的方程为
，离心率
，且短轴长为4．
求椭圆的方程；
已知
，
，若直线l与圆
相切，且交椭圆E于C、D两点，记
的面积为
，记
的面积为
，求
的最大值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某中学利用周末组织教职员工进行了一次秋季登山健身的活动，有Ⅳ人参加，现将所有参加者按年龄情况分为
，
，
，
，
，
，
等七组，其频率分布直方图如图所示，已知这组的参加者是6人．
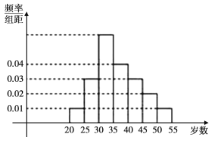
（1）已知和这两组各有2名数学教师，现从这两个组中各选取2人担任接待工作，设两组的选择互不影响，求两组选出的人中恰有1名数学老师的概率；
（2）组织者从
这组的参加者（其中共有4名女教师，其余全为男教师）中随机选取3名担任后勤保障工作，其中女教师的人数为
，求的分布列和均值．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】《中国诗词大会》（第三季）亮点颇多，在“人生自有诗意”的主题下，十场比赛每场都有一首特别设计的开场诗词在声光舞美的配合下，百人团齐声朗诵，别有韵味.若《沁园春·长沙》、《蜀道难》、《敕勒歌》、《游子吟》、《关山月》、《清平乐·六盘山》排在后六场，且《蜀道难》排在《游子吟》的前面，《沁园春·长沙》与《清平乐·六盘山》不相邻且均不排在最后，则后六场的排法有__________种．（用数字作答）
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
