数列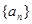 的项是由1或2构成,且首项为1,在第
的项是由1或2构成,且首项为1,在第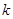 个1和第
个1和第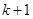 个1之间有
个1之间有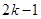 个2,即数列
个2,即数列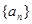 为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列
为:1,2,1,2,2,2,1,2,2,2,2,2,1,…,记数列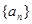 的前
的前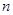 项和为
项和为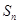 ,则
,则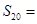 ;
;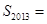 .
.
【答案】
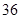 ;
;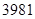
【解析】
试题分析:前20个数中,有4个1,16个2,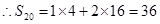 ;将数列1,2,1,2,2,2,1,2,2,2,2,2,1,…,进行适当地加括号(1,2),(1,2,2,2,),(1,2,2,2,2,2,),(1,…,2),…,即从第
;将数列1,2,1,2,2,2,1,2,2,2,2,2,1,…,进行适当地加括号(1,2),(1,2,2,2,),(1,2,2,2,2,2,),(1,…,2),…,即从第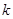 个1到第
个1到第 个1前的所有数用一个括号包围起来,则第
个1前的所有数用一个括号包围起来,则第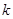 个括号里面有1个1,
个括号里面有1个1,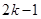 个2,第
个2,第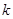 个括号中共
个括号中共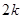 个数,则加括号后第
个数,则加括号后第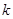 个括号中最后一个数对应原数列的序数
个括号中最后一个数对应原数列的序数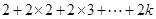
 ,设原数列第2013个数处于加括号后的第
,设原数列第2013个数处于加括号后的第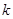 个括号中,则有
个括号中,则有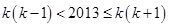 ,由于
,由于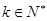 ,解得
,解得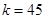 ,即前2013个数中共有45个1,1968个2,
,即前2013个数中共有45个1,1968个2,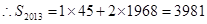 .
.
考点:推理与证明,数列求和

