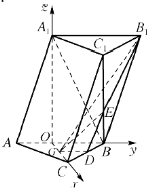
【题目】如图,在三棱柱![]() 中,
中,![]() 为
为![]() 的重心,
的重心,![]() .
.

(1)求证:![]()
![]() 平面
平面![]() ;
;
(2)若侧面![]()
![]() 底面
底面![]() ,
,![]() ,
,![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值.
的正弦值.
参考答案:
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连接![]() ,并延长
,并延长![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,分别连接
,分别连接![]() ,
,![]() .为
.为![]() 是
是![]() 的重心,所以
的重心,所以![]() ,又
,又![]() ,所以
,所以![]() ,所以
,所以![]() ,从而
,从而![]() 平面
平面![]() ;(2)以
;(2)以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,利用直线
轴建立空间直角坐标系,利用直线![]() 的方向向量与平面
的方向向量与平面![]() 的法向量,计算得线面角的正弦值为
的法向量,计算得线面角的正弦值为![]() .
.
试题解析:
(1)连接![]() ,并延长
,并延长![]() ,交
,交![]() 于点
于点![]() ,过
,过![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,分别连接
,分别连接![]() ,
,![]() .因为
.因为![]() 是
是![]() 的重心,所以
的重心,所以![]() .
.
又![]() ,所以
,所以![]() .
.
又据三棱柱![]() 性质知
性质知![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以![]() .
.
又![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
又因为![]() ,
,![]() ,
,
所以平面![]()
![]() 平面
平面![]()
又因为![]() ,
,
所以![]()
![]() 平面
平面![]()
(2)连结![]() .
.
因为![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,
所以![]() ,所以
,所以![]() .
.
因为侧面![]()
![]() 底面
底面![]() ,侧面
,侧面![]() 底面
底面![]()
![]() ,
,![]() ,
,
所以![]()
![]() 平面
平面![]() .
.
因为![]() ,
,![]() ,所以
,所以![]() 是等边三角形,
是等边三角形,
所以![]() .
.
以![]() 为原点,分别以
为原点,分别以![]() ,
,![]() ,
,![]() 为
为![]() 轴,
轴,![]() 轴,
轴,![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() ,
,![]() ,
,![]() ,
,![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则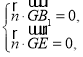
所以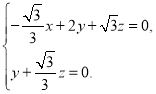
令![]() ,得
,得![]() ,
,
所以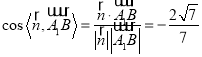 .
.
所以![]() .即直线
.即直线![]() 与平面
与平面![]() 所成角
所成角![]() 的正弦值为
的正弦值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,(
,( 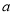 为实数),
为实数),
(1)讨论函数
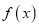 的单调区间;
的单调区间;(2)求函数
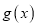 的极值;
的极值;(3)求证:
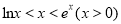
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列方程,并回答问题:
①
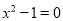 ;②
;② ;③
;③ ;④
;④ ;…
;…(1)请你根据这列方程的特点写出第
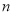 个方程;
个方程;(2)直接写出第2009个方程的根;
(3)说出这列方程的根的一个共同特点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】给出下列四个关于数列命题:
(1)若
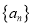 是等差数列,则三点
是等差数列,则三点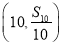 、
、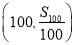 、
、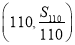 共线;
共线;(2)若
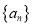 是等比数列,则
是等比数列,则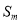 、
、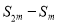 、
、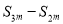 (
(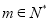 )也是等比数列;
)也是等比数列;(3)等比数列
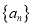 的前n项和为
的前n项和为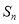 ,若对任意的
,若对任意的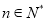 ,点
,点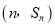 均在函数
均在函数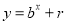 (
(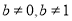 ,
, 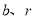 均为常数)的图象上,则r的值为
均为常数)的图象上,则r的值为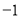 .
.(4)对于数列
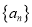 ,定义数列
,定义数列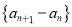 为数列
为数列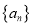 的“差数列”,若
的“差数列”,若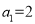 ,
, 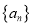 的“差数列”的通项为
的“差数列”的通项为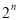 ,则数列
,则数列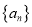 的前
的前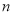 项和
项和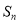
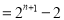
其中正确命题的个数是 ( )
A. 4 B. 3 C. 2 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (
( ).
).(1)若曲线
 在点
在点 处与直线
处与直线 相切,求
相切,求 的值;
的值;(2)若函数
 有两个零点
有两个零点 ,
, ,试判断
,试判断 的符号,并证明.
的符号,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l经过点
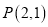 ,则
,则(1)若直线l与x轴、y轴的正半轴分别交于A、B两点,且△OAB的面积为4,求直线l的方程;
(2)若直线l与原点距离为2,求直线l的方程.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 ,
,  其中
其中 ,
,(1)若
 是函数
是函数 的极值点,求实数
的极值点,求实数 的值及
的值及 的单调区间;
的单调区间;(2)若对任意的
 ,
,  使得
使得 恒成立,且
恒成立,且 ,求实数
,求实数 的取值范围.
的取值范围.
相关试题

