证明题:如图:两直线a,b平行,直线c与a,b相交,则:直线a、b、c三线共面(要求写处已知、求证、证明)
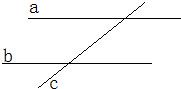

已知:a∥b,a∩c=A,b∩c=B,
求证:直线a、b、c共面.
证明:∵a∥b
∴a与b确定一个平面α
又a∩c=A,b∩c=B,
则A∈α,B∈α
∴AB?α,即c?α,
∴直线a、b、c共面.
求证:直线a、b、c共面.
证明:∵a∥b
∴a与b确定一个平面α
又a∩c=A,b∩c=B,
则A∈α,B∈α
∴AB?α,即c?α,
∴直线a、b、c共面.

