【题目】一个盒子里装有标号1、2、3、4的4张形状大小完全相同的标签,先后随机地选取两张标签,根据下列条件,分别求两张标签上的数字为相邻整数的概率.
(1)标签的选取是无放回的;
(2)标签的选取是有放回的.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
试题分析:(1)记事件![]() “选取的两张标签上的数字为相邻整数”,列出基本事件的个数,即可利用古典概型的概率计算公式求解概率;(2)列出从
“选取的两张标签上的数字为相邻整数”,列出基本事件的个数,即可利用古典概型的概率计算公式求解概率;(2)列出从![]() 张标签中有放回随机选取
张标签中有放回随机选取![]() 张,构成的基本事件的个数,进而得到事件
张,构成的基本事件的个数,进而得到事件![]() 所包含的基本事件的个数,利用古典概型及其概率的计算公式,求解概率.
所包含的基本事件的个数,利用古典概型及其概率的计算公式,求解概率.
试题解析:记事件![]() “选取的两张标签上的数字为相邻整数”.
“选取的两张标签上的数字为相邻整数”.
(1)从4张标签中无放回随机选取2张,共12个基本事件,分别为![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
事件![]() 包含了其中的6个基本事件:
包含了其中的6个基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由古典概型概率计算公式知:![]() ,
,
故无放回地选取两张标签,其上数字为相邻整数的概率为![]() .
.
(2)从4张标签中有放回随机选取2张,共16个基本事件,分别为:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
事件![]() 包含了其中的6个基本事件:
包含了其中的6个基本事件:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
由古典概型概率计算公式知:![]() ,
,
故有放回选取2张标签,其上数字为相邻整数的概率为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 的图象关于直线
的图象关于直线 对称.
对称.(1)求实数
 的值;
的值;(2)若对任意的
 ,使得
,使得 有解,求实数
有解,求实数 的取值范围;
的取值范围;(3)若
 时,关于
时,关于 的方程
的方程 有四个不等式的实根,求实数
有四个不等式的实根,求实数 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆
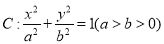 的两个焦点为
的两个焦点为 ,
,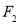 ,离心率为
,离心率为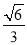 ,点
,点 ,
,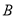 在椭圆上,
在椭圆上, 在线段
在线段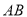 上,且
上,且 的周长等于
的周长等于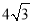 .
.(1)求椭圆
 的标准方程;
的标准方程;(2)过圆
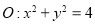 上任意一点
上任意一点 作椭圆
作椭圆 的两条切线
的两条切线 和
和 与圆
与圆 交于点
交于点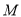 ,
,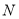 ,求
,求 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】在直角坐标系中,以坐标原点
 为极点,
为极点,  轴的非负半轴为极轴建立极坐标系.已知点
轴的非负半轴为极轴建立极坐标系.已知点 的极坐标为
的极坐标为 ,曲线
,曲线 的参数方程为
的参数方程为 为参数).
为参数).(1)直线
 过
过 且与曲线
且与曲线 相切,求直线
相切,求直线 的极坐标方程;
的极坐标方程;(2)点
 与点
与点 关于
关于 轴对称,求曲线
轴对称,求曲线 上的点到点
上的点到点 的距离的取值范围.
的距离的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一块半径为
 的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池
的正常数)的半圆形空地,开发商计划征地建一个矩形的游泳池 和其附属设施,附属设施占地形状是等腰
和其附属设施,附属设施占地形状是等腰 ,其中
,其中 为圆心,
为圆心, 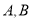 在圆的直径上,
在圆的直径上,  在半圆周上,如图.
在半圆周上,如图.(1)设
 ,征地面积为
,征地面积为 ,求
,求 的表达式,并写出定义域;
的表达式,并写出定义域;(2)当
 满足
满足 取得最大值时,开发效果最佳,求出开发效果最佳的角
取得最大值时,开发效果最佳,求出开发效果最佳的角 的值,
的值,求出
 的最大值.
的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四棱锥
 中,侧棱
中,侧棱 ,底面
,底面 为直角梯形,其中
为直角梯形,其中 ,
, .
.
(1)求证:侧面PAD⊥底面ABCD;
(2)求三棱锥
 的表面积.
的表面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线
 (
( ).
).(1)求直线
 经过的定点坐标;
经过的定点坐标;(2)若直线
 交
交 负半轴于
负半轴于 ,交
,交 轴正半轴于
轴正半轴于 ,
, 为坐标系原点,
为坐标系原点, 的面积为
的面积为 ,求
,求 的最小值并求此时直线
的最小值并求此时直线 的方程.
的方程.
相关试题

