
【题目】[选修4―4:坐标系与参数方程]
在直角坐标系xOy中,曲线C的参数方程为![]() (θ为参数),直线l的参数方程为
(θ为参数),直线l的参数方程为![]() .
.
(1)若a=1,求C与l的交点坐标;
(2)若C上的点到l的距离的最大值为![]() ,求a.
,求a.
【答案】(1)![]() 与
与![]() 的交点坐标为
的交点坐标为![]() ,
, ![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】试题分析:(1)直线与椭圆的参数方程化为直角坐标方程,联立解交点坐标;(2)利用椭圆参数方程,设点![]() ,由点到直线距离公式求参数.
,由点到直线距离公式求参数.
试题解析:(1)曲线![]() 的普通方程为
的普通方程为![]() .
.
当![]() 时,直线
时,直线![]() 的普通方程为
的普通方程为![]() .
.
由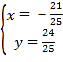 解得
解得![]() 或
或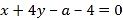 .
.
从而![]() 与
与![]() 的交点坐标为
的交点坐标为![]() ,
, ![]() .
.
(2)直线![]() 的普通方程为
的普通方程为![]() ,故
,故![]() 上的点
上的点![]() 到
到![]() 的距离为
的距离为
![]() .
.
当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .由题设得
.由题设得![]() ,所以
,所以![]() ;
;
当![]() 时,
时, ![]() 的最大值为
的最大值为![]() .由题设得
.由题设得![]() ,所以
,所以![]() .
.
综上, ![]() 或
或![]() .
.
点睛:本题为选修内容,先把直线与椭圆的参数方程化为直角坐标方程,联立方程,可得交点坐标,利用椭圆的参数方程,求椭圆上一点到一条直线的距离的最大值,直接利用点到直线的距离公式,表示出椭圆上的点到直线的距离,利用三角有界性确认最值,进而求得参数![]() 的值.
的值.


 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实常数).
为实常数).

(1)当![]() 时,作出
时,作出![]() 的图象,并写出它的单调递增区间;
的图象,并写出它的单调递增区间;
(2)设![]() 在区间
在区间![]() 的最小值为
的最小值为![]() ,求
,求![]() 的表达式;
的表达式;
(3)设![]() ,若函数
,若函数![]() 在区间
在区间![]() 上是增函数,求实数
上是增函数,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合![]() 集合
集合![]() ,集合
,集合![]() ,且集合D满足
,且集合D满足![]() .
.
(1)求实数a的值.
(2)对集合![]() ,其中
,其中![]() ,定义由
,定义由![]() 中的元素构成两个相应的集合:
中的元素构成两个相应的集合:![]() ,
,![]() ,其中
,其中![]() 是有序实数对,集合S和T中的元素个数分别为
是有序实数对,集合S和T中的元素个数分别为![]() 和
和![]() ,若对任意的
,若对任意的![]() ,总有
,总有![]() ,则称集合
,则称集合![]() 具有性质P.
具有性质P.
①请检验集合![]() 是否具有性质P,并对其中具有性质P的集合,写出相应的集合S和T.
是否具有性质P,并对其中具有性质P的集合,写出相应的集合S和T.
②试判断m和n的大小关系,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图.在四棱锥![]() 中,
中,![]() ,
,![]() ,
,![]() 平面ABCD,且
平面ABCD,且![]() .
.![]() ,
,![]() ,M、N分别为棱PC,PB的中点.
,M、N分别为棱PC,PB的中点.

(1)证明:A,D,M,N四点共面,且![]() 平面ADMN;
平面ADMN;
(2)求直线BD与平面ADMN所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知某地每单位面积菜地年平均使用氮肥量x(单位:kg)与每单位面积蔬菜年平均产量Y(单位:t)之间的关系有如下数据:
年份 | 2000 | 2001 | 2002 | 2003 | 2004 | 2005 | 2006 | 2007 |
x/kg | 70 | 74 | 80 | 78 | 85 | 92 | 90 | 95 |
Y/t | 5.1 | 6.0 | 6.8 | 7.8 | 9.0 | 10.2 | 10.0 | 12.0 |
年份 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | |
x/kg | 92 | 108 | 115 | 123 | 130 | 138 | 145 | |
Y/t | 11.5 | 11.0 | 11.8 | 12.2 | 12.5 | 12.8 | 13.0 |
(1)求x与Y之间的相关系数,并检验是否线性相关;
(2)若线性相关,求每单位面积蔬菜年平均产量Y与每单位面积菜地年平均使用氮肥量x之间的回归直线方程,并估计每单位面积菜地年平均使用氮肥150 kg时,每单位面积蔬菜的年平均产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
(1)(坐标系与参数方程选做题)曲线C的直角坐标方程为x2+y2﹣2x=0,以原点为极点,x轴的正半轴为极轴建立积坐标系,则曲线C的极坐标方程为 .
(2)(不等式选做题)在实数范围内,不等式|2x﹣1|+|2x+1|≤6的解集为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com