

【题目】在某超市,随机调查了100名顾客购物时使用手机支付的情况,得到如下的![]() 列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为
列联表,已知从其中使用手机支付的人群中随机抽取1人,抽到青年的概率为![]() .
.
青年 | 中老年 | 合计 | |
使用手机支付 | 60 | ||
不使用手机支付 | 28 | ||
合计 | 100 |
(1)根据已知条件完成![]() 列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
列联表,并根据此资料判断是否有99.9%的把握认为“超市购物用手机支付与年龄有关”.
(2)现按照“使用手机支付”和“不使用手机支付”进行分层抽样,从这100名顾客中抽取容量为5的样本,求“从样本中任选3人,则3人中至少2人使用手机支付”的概率.
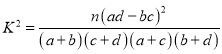 (其中
(其中 ![]() )
)
【答案】(1)列联表见解析,有;(2)![]()
【解析】
(1)根据已知条件求出老年的人数,青年的人数,即可完成![]() 列联表,并根据此资料求出
列联表,并根据此资料求出![]() ,即可判断是否有
,即可判断是否有![]() 的把握认为“超市购物用手机支付与年龄有关”.
的把握认为“超市购物用手机支付与年龄有关”.
(2)这100名顾客中采用分层抽样从“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本中:使用手机支付的人有3人,记编号为1,2,3;不使用手机支付的人有2人,记编号为![]() ,
,![]() ,列出事件数目,然后求解至少有2人是不使用手机支付的概率.
,列出事件数目,然后求解至少有2人是不使用手机支付的概率.
解:(1)![]() 从使用手机支付的人群中随机抽取1人,抽到青年的概率为
从使用手机支付的人群中随机抽取1人,抽到青年的概率为![]()
![]() 使用手机支付的人群中的青年的人数为
使用手机支付的人群中的青年的人数为![]() 人,
人,
青年 | 中老年 | 合计 | |
使用手机支付 | 48 | 12 | 60 |
不使用手机支付 | 12 | 28 | 40 |
合计 | 60 | 40 | 100 |
则使用手机支付的人群中的中老年的人数为![]() 人,所以
人,所以![]() 列联表为:
列联表为:

故有99.9%的把握认为“市场购物用手机支付与年龄有关”.
(2)这100名顾客中采用分层抽样从“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本中:
使用手机支付的人有![]() 人,
人,
使用手机支付的人有3人,记编号为1,2,3;不使用手机支付的人有2人,记编号为![]() ,
,![]() ,
,
则从这个样本中任选3人有
![]() 共10种
共10种
其中至少有2人是使用手机支付的
![]() 共7种,
共7种,
故所求概率为![]()


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() 的焦距为
的焦距为![]() ,直线
,直线![]() 截圆
截圆![]() 与椭圆
与椭圆![]() 所得的弦长之比为
所得的弦长之比为![]() ,圆
,圆![]() 、椭圆
、椭圆![]() 与
与![]() 轴正半轴的交点分别为
轴正半轴的交点分别为![]() ,
,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() (
(![]() 且
且![]() )为椭圆
)为椭圆![]() 上一点,点
上一点,点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,直线
,直线![]() ,
,![]() 分别交
分别交![]() 轴于点
轴于点![]() ,
,![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】祖暅原理也就是“等积原理”,它是由我国南北朝杰出的数学家祖冲之的儿子祖暅首先提出来的.祖暅原理的内容是:“幂势既同,则积不容异”,“势”即是高,“幂”是面积.意思是,如果夹在两平行平面间的两个几何体,被平行于这两个平行平面的平面所截,如果两个截面的面积总相等,那么这两个几何体的体积相等.已知,两个平行平面间有三个几何体,分别是三棱锥、四棱锥、圆锥(高度都是h),其中:三棱锥的体积为V,四棱锥的底面是边长为a的正方形,圆锥的底面半径为r,现用平行于这两个平面的平面去截三个几何体,如果得到的三个截面面积总相等,那么,下面关系式正确的是( )
A.![]() ,
,![]() ,
,![]() B.
B.![]() ,
,![]() ,
,![]()
C.![]() ,
,![]() ,
,![]() D.
D.![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
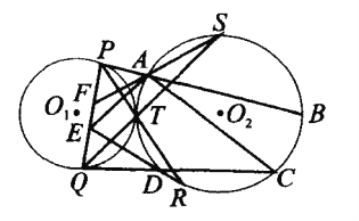
【题目】如图,两圆外切于点T, PQ为![]() 的弦,直线PT、QT分别交
的弦,直线PT、QT分别交![]() 于点R、S,分别过P、Q作
于点R、S,分别过P、Q作![]() 的切线依次交
的切线依次交![]() 于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:
于A、B、D、C,直线RD、SA分别交PQ于E、F。求证:![]() 。
。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知向量![]() ,
,![]() ,设函数
,设函数![]() ,且
,且![]() 的图象过点
的图象过点![]() 和点
和点![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 的最大值和最小值及相应的
的最大值和最小值及相应的![]() 的值;
的值;
(2)将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的4倍,纵坐标不变,得到函数![]() 的图象,若
的图象,若![]() 在
在![]() 有两个不同的解,求实数
有两个不同的解,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() 的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
的焦点为F,过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N。
(1)求证:直线MN必过定点;
(2)分别以AB和CD为直径作圆,求两圆相交弦中点H的轨迹方程。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高二年段的男生进行体检,现将高二男生的体重(kg)数据进行整理后分成6组,并绘制部分频率分布直方图(如图所示).已知第三组[60,65)的人数为200.根据一般标准,高二男生体重超过65kg属于偏胖,低于55kg属于偏瘦.观察图形的信息,回答下列问题:

(1)求体重在[60,65)内的频率,并补全频率分布直方图;
(2)用分层抽样的方法从偏胖的学生中抽取6人对日常生活习惯及体育锻炼进行调查,则各组应分别抽取多少人?
(3)根据频率分布直方图,估计高二男生的体重的中位数与平均数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将直角三角形![]() 沿斜边上的高
沿斜边上的高![]() 折成
折成![]() 的二面角,已知直角边
的二面角,已知直角边![]() ,那么下面说法正确的是_________.
,那么下面说法正确的是_________.
(1) 平面![]() 平面
平面![]() (2)四面体
(2)四面体![]() 的体积是
的体积是![]()
(3)二面角![]() 的正切值是
的正切值是![]() (4)
(4)![]() 与平面
与平面![]() 所成角的正弦值是
所成角的正弦值是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com