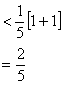已知点Pn(an,bn)都在直线：y=2x+2上，P1为直线与x轴的交点，数列 成等差数列，公差为1.（n∈N+）

（1）求数列，的通项公式；

（2）若f(n)=   问是否存在k,使得f(k+5)=2f(k)－2成立；若存在，求出k的值，若不存在，说明理由。

（3）求证：      （n≥2，n∈N+）

解:(1) P    ∴  ∴　

(2) 若k为奇数                     若k为偶数

则f(k)=              则f(k)=2k－2

f(k+5)=b            f(k+5)=k+3

2k+8=2k－4－2                 k+3=4k－4－2

 无解：                         9=3k

这样的k不存在                 k=3(舍去)无解

（3）

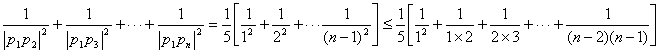              =     n

关闭