搜索
【题目】已知椭圆
的焦距为2，过右焦点和短轴一个端点的直线的斜率为
，
为坐标原点.
（1）求椭圆
的方程；
（2）设点
，直线
与椭圆C交于两个不同点P，Q，直线AP与x轴交于点M，直线AQ与x轴交于点N，若|OM|·|ON|=2，求证：直线l经过定点.
【答案】（1）
；（2）详见解析.
【解析】
（1）由题意
，根据过右焦点和短轴一个端点的直线的斜率为
，求出
，求出
，即得椭圆
的方程；
（2）设
.把直线
的方程代入椭圆的方程，韦达定理.写出直线
和直线
的方程，求出
.根据
，求出
的值，即可证明直线l经过定点.
（1）由题意，得椭圆的半焦距，右焦点
，上顶点
，所以直线
的斜率
，解得
，由
，得
，所以椭圆的方程为.
（2）设.
联立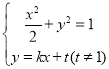
得
，
，
，
.
直线
，令
得
，即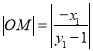
；
同理可得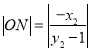
.
因为，所以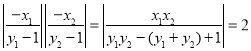
；
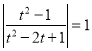，解之得只有
满足题意，所以直线方程为
，所以直线恒过定点
.
