【题目】已知函数![]() ,
, ![]() .
.
(1)若函数![]() 有三个不同的极值点,求
有三个不同的极值点,求![]() 的值;
的值;
(2)若存在实数![]() ,使对任意的
,使对任意的![]() ,不等式
,不等式![]() 恒成立,求正整数
恒成立,求正整数![]() 的最大值.
的最大值.
参考答案:
【答案】(Ⅰ)![]() 的取值范围是
的取值范围是![]() ;(Ⅱ)正整数
;(Ⅱ)正整数![]() 的最大值为5.
的最大值为5.
【解析】试题分析:(Ⅰ)求出![]() 的导函数,
的导函数, ![]() 有3个极值点等价于方程
有3个极值点等价于方程![]() 有3个根;令
有3个根;令![]() ,根据
,根据![]() 的单调性可知
的单调性可知![]() 有3个零点,则
有3个零点,则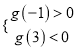 ,解出
,解出![]() 的取值范围即可;(Ⅱ)不等式
的取值范围即可;(Ⅱ)不等式![]() ,即
,即![]() ,分离参数得
,分离参数得![]() .
.
转化为存在实数![]() ,使对任意的
,使对任意的![]() ,不等式
,不等式![]() 恒成立;构造新函数,确定单调性,计算相应函数值的正负,即可求正整数
恒成立;构造新函数,确定单调性,计算相应函数值的正负,即可求正整数![]() 的最大值.
的最大值.
试题解析:(Ⅰ) ![]()
∵![]() 有3个极值点,∴
有3个极值点,∴![]() 有3个根
有3个根
令![]()
![]() 在
在![]() 上递增,
上递增, ![]() 上递减.
上递减.
∴![]() 有3个零点,∴
有3个零点,∴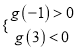 ,∴
,∴![]()
(Ⅱ)不等式![]() ,即
,即![]() ,即
,即![]() .
.
转化为存在实数![]() ,使对任意的
,使对任意的![]() ,
,
不等式![]() 恒成立.
恒成立.
即不等式![]() 在
在![]() 上恒成立.
上恒成立.
即不等式![]() 在
在![]() 上恒成立
上恒成立
设![]() ,则
,则![]() .
.
设![]() ,则
,则![]() ,因为
,因为![]() ,有
,有![]() .
.
故![]() 在区间
在区间![]() 上是减函数;
上是减函数;
又![]()
故存在![]() ,使得
,使得![]() .
.
当![]() 时,有
时,有![]() ,当
,当![]() 时,有
时,有![]() .
.
从而![]() 在区间
在区间![]() 上递增,在区间
上递增,在区间![]() 上递减
上递减
又![]() ,
,
![]() .
.
所以当![]() 时,恒有
时,恒有![]() ;当
;当![]() 时,恒有
时,恒有![]() ;
;
故使命题成立的正整数![]() 的最大值为5.
的最大值为5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知定义在R上的奇函数,当x>0时,f(x)=x2+2x﹣1
(1)求f(﹣3)的值;
(2)求函数f(x)的解析式. -
科目: 来源: 题型:
查看答案和解析>>【题目】轴截面是边长为4
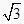 的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为
的等边三角形的圆锥的直观图如图所示,过底面圆周上任一点作一平面α,且α与底面所成的二面角为 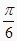 ,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( )
,已知α与圆锥侧面交线的曲线为椭圆,则此椭圆的离心率为( ) 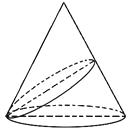
A.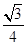
B.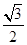
C.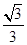
D.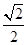
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A为左顶点,F是左焦点,l交OA的延长线于点B,点P,Q在椭圆上,有PD⊥l于点D,QF⊥AO,则椭圆的离心率是①
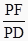 ; ②
; ② 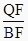 ; ③
; ③ 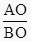 ; ④
; ④ 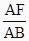 ; ⑤
; ⑤  其中正确的是( )
其中正确的是( )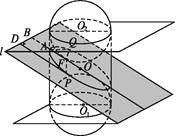
A.①②
B.①③④
C.②③⑤
D.①②③④⑤ -
科目: 来源: 题型:
查看答案和解析>>【题目】[选修4―4:坐标系与参数方程]
在平面直角坐标系中,以坐标原点
 为极点,
为极点,  轴的正半轴为极轴建立极坐标系.已知直线
轴的正半轴为极轴建立极坐标系.已知直线 的参数方程为
的参数方程为 ;曲线
;曲线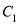 的极坐标方程为
的极坐标方程为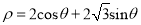 ;曲线
;曲线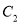 的参数方程为
的参数方程为 (
(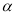 为参数).
为参数).(1)求直线
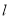 的直角坐标方程、曲线
的直角坐标方程、曲线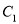 的直角坐标方程和曲线
的直角坐标方程和曲线 的普通方程;
的普通方程;(2)若直线
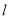 与曲线
与曲线 曲线
曲线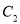 在第一象限的交点分别为
在第一象限的交点分别为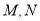 ,求
,求 之间的距离.
之间的距离. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
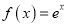 ,
, 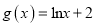 .
.(1)若直线
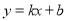 是曲线
是曲线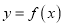 与曲线
与曲线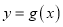 的公切线,求
的公切线,求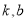 ;
;(2)设
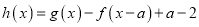 ,若
,若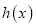 有两个零点,求
有两个零点,求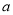 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】在底面半径为6的圆柱内,有两个半径也为6的球面,两球的球心距为13,若作一个平面与两个球都相切,且与圆柱面相交成一椭圆,则椭圆的长轴长为。
相关试题

