(1)由已知f'(x)=a+bcosx,于是得:
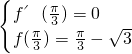
代入可得:a=1,b=-2…(3分)
(2)由f'(x)=1-2cosx=1,得cosx=0,当
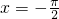
时,cosx=0此时
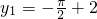
,
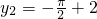
,y
1=y
2所以
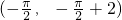
是直线l与曲线S的一个切点,当
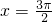
时,cosx=0,
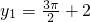
,
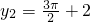
,y
1=y
2所以
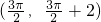
是直线l与曲线S的一个切点 所以直线l与曲线S相切且至少有两个切点…(6分)
对任意x∈R,g(x)-F(x)=(x+2)-(x-2sinx)=2+2sinx≥0
所以g(x)≥F(x),因此直线l:y=x+2是曲线S:y=ax+bsinx的“上夹线”…(9分)
(3)方法一:
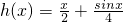
,x
1为
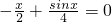
的根,即x
1=0,也即|x
3|<1,|x
2|<1…(10分)
而
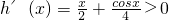
∴
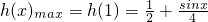
,
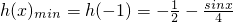
∴
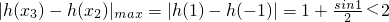
…(13分)
所以存在这样最小正整数M=2使得|h(x
3)-h(x
2)|≤M恒成立.…(14分)
方法二:不妨设x
2<x
3,因为h'(x)>0,所以h(x)为增函数,所以h(x
2)<h(x
3)
又因为h'(x)-1<0,所以h(x)-x为减函数,所以h(x
2)-x
2>h(x
3)-x
3所以0<h(x
3)-h(x
2)<x
3-x
2,…(11分)
即|h(x
3)-h(x
2)|<|x
3-x
2|=|x
3-x
1-(x
2-x
1)|≤|x
3-x
1|+|x
2-x
1|<2…(13分)
故存在最小正整数M=2,使得|h(x
3)-h(x
2)|≤M恒成立…(14分)
分析:(1)根据题意,求出函数的导数再代入可得方程组,求解即可;
(2)设直线l:g(x)=x+2,曲线S:f(x)=ax+bsinx,求出f(x)的导数,因为直线斜率为1,由f'(x)=1-2cosx=1可得极值点,再验证得到直线与曲线f(x)的切点,利用g(x)≥F(x)也可作差得到结论.
(3)本问可求出h(x)的最大值和最小值然后转化为|h(x
3)-h(x
2)|
max=|h(x)
max-h(x)
min|小于某个正整数M即可;本问题也可以利用函数的单调性来求解,只需做一个转化h(x)与x的关系,为此可构造函数h(x)-x,于是可以证得结论.
点评:考查函数的导数以及导数的应用:求函数的极值,最值判断极值存在的条件,本题中的(2)和(3)是一种新定义问题,如果对定义以及本题题意把握不准,难免会出差错,甚至无从下手,这就需要多角度分析,比如数形结合来分析,再者关键是深刻理解性定义,这样就能容易解答;第(3)问较为综合,是一类新颖的函数问题,解答本题转化与划归是精髓,另外结合要证明的不等式之特点,构造函数不失为一种好思维,好方法.

 时,f(x)取得极小值
时,f(x)取得极小值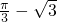 .
.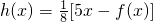 ,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.
,设x1是方程h(x)-x=0的实数根,若对于h(x)定义域中任意的x2、x3,当|x2-x1|<1,且|x3-x1|<1时,问是否存在一个最小的正整数M,使得|h(x3)-h(x2)|≤M恒成立,若存在请求出M的值;若不存在请说明理由.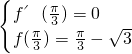 代入可得:a=1,b=-2…(3分)
代入可得:a=1,b=-2…(3分)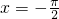 时,cosx=0此时
时,cosx=0此时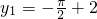 ,
,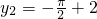 ,y1=y2所以
,y1=y2所以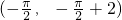 是直线l与曲线S的一个切点,当
是直线l与曲线S的一个切点,当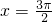 时,cosx=0,
时,cosx=0,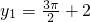 ,
,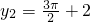 ,y1=y2
,y1=y2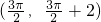 是直线l与曲线S的一个切点 所以直线l与曲线S相切且至少有两个切点…(6分)
是直线l与曲线S的一个切点 所以直线l与曲线S相切且至少有两个切点…(6分)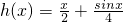 ,x1为
,x1为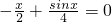 的根,即x1=0,也即|x3|<1,|x2|<1…(10分)
的根,即x1=0,也即|x3|<1,|x2|<1…(10分)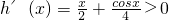 ∴
∴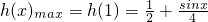 ,
,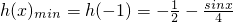
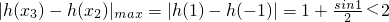 …(13分)
…(13分)
