【题目】已知函数f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)当a=﹣ ![]() 时,求函数f(x)的极值;
时,求函数f(x)的极值;
(Ⅱ)当a>0时,求函数g(x)的单调区间;
(Ⅲ)当x∈[1,+∞)时,若y=f(x)图象上的点都在 ![]() 所表示的平面区域内,求实数a的取值范围.
所表示的平面区域内,求实数a的取值范围.
参考答案:
【答案】解:(Ⅰ)当a=﹣ ![]() 时,f(x)=﹣
时,f(x)=﹣ ![]() x2+
x2+ ![]() x+lnx+
x+lnx+ ![]() ,
,
f(x)的定义域为(0,+∞),f′(x)=﹣ ![]() ;
;
列表讨论f′(x)和f(x)的变化情况:
x | (0,2) | 2 | (2,+∞) |
f′(x) | + | 0 | ﹣ |
f(x) | ↗ | 极大值 | ↘ |
∴当x=2时,f(x)取得极大值f(2)=ln2+ ![]() ;
;
(Ⅱ)当a>0时,g(x)=ax2﹣(2a+1)x+lnx+a+1,
g(x)的定义域为(0,+∞),
g′(x)= 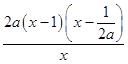 ,
,
令g′(x)=0,得x=1或x= ![]() ,
,
①当0<a< ![]() ,即
,即 ![]() >1时,
>1时,
由g′(x)<0,解得:1<x< ![]() ,
,
由g′(x)>0,解得:0<x<1或x> ![]() ,
,
∴g(x)在(1, ![]() )上单调递减,
)上单调递减,
在(0,1),( ![]() ,+∞)上单调递增;
,+∞)上单调递增;
②当a= ![]() ,即
,即 ![]() =1时,在(0,+∞)上,g′(x)≥0,
=1时,在(0,+∞)上,g′(x)≥0,
∴g(x)在(0,+∞)上单调递增;
③当a> ![]() ,即0<
,即0< ![]() <1时,
<1时,
由g′(x)<0,解得 ![]() <x<1,由g′(x)>0,解得0<x<
<x<1,由g′(x)>0,解得0<x< ![]() 或x>1,
或x>1,
∴g(x)在( ![]() ,1)上单调递减,
,1)上单调递减,
在(0, ![]() ),(1,+∞)上单调递增.
),(1,+∞)上单调递增.
(Ⅲ)∵y=f(x)图象上的点都在 ![]() 所表示的平面区域内,
所表示的平面区域内,
∴当x∈[1,+∞)时,f(x)﹣x≤0恒成立,
即当x∈[1,+∞)时,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立.
只需g(x)max≤0;
①当a>0时,由(Ⅱ)知,
当0<a< ![]() 时,g(x)在(1,
时,g(x)在(1, ![]() )上单调递减,在(
)上单调递减,在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
∴g(x)在[1,+∞)上无最大值,不满足条件;
当a≥ ![]() 时,g(x) 在(1,+∞)上单调递增,
时,g(x) 在(1,+∞)上单调递增,
∴g(x)在[1,+∞)上无最大值,不满足条件;
②当a=0时,g′(x)=﹣ ![]() ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上单调递减,g(x)≤g(1)=0成立;
③当a<0时,g′(x)= 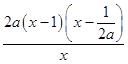 ,在(1,+∞)上,g′(x)<0,
,在(1,+∞)上,g′(x)<0,
∴g(x)在[1,+∞)上单调递减,g(x)≤g(1)=0成立,
综上可知,实数a的取值范围是a≤0
【解析】(Ⅰ)求出函数的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极大值即可;(Ⅱ)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;(Ⅲ)问题转化为x∈[1,+∞)时,g(x)=a(x﹣1)2+lnx+1﹣x≤0恒成立,只需g(x)max≤0即可,根据函数的单调性求出a的范围.
【考点精析】利用利用导数研究函数的单调性和函数的极值与导数对题目进行判断即可得到答案,需要熟知一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在四棱锥P﹣ABCD中,AB∥CD,AB⊥AD,AB=AD=AP=2CD=2,M是棱PB上一点.
(Ⅰ)若BM=2MP,求证:PD∥平面MAC;
(Ⅱ)若平面PAB⊥平面ABCD,平面PAD⊥平面ABCD,求证:PA⊥平面ABCD;
(Ⅲ)在(Ⅱ)的条件下,若二面角B﹣AC﹣M的余弦值为 ,求
,求 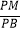 的值.
的值.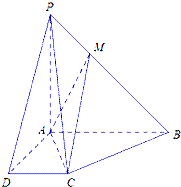
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数列{an}是等差数列,Sn为{an}的前n项和,且a10=19,S10=100;数列{bn}对任意n∈N* , 总有b1b2b3…bn﹣1bn=an+2成立.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)记cn=(﹣1)n ,求数列{cn}的前n项和Tn .
,求数列{cn}的前n项和Tn . -
科目: 来源: 题型:
查看答案和解析>>【题目】已知椭圆C:
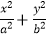 =1(a>b>0)的短轴长为2,离心率e=
=1(a>b>0)的短轴长为2,离心率e= 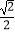 .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)若直线l:y=kx+m与椭圆交于不同的两点A,B,与圆x2+y2= 相切于点M.
相切于点M.
(i)证明:OA⊥OB(O为坐标原点);
(ii)设λ=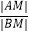 ,求实数λ的取值范围.
,求实数λ的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
 .
.(1)当
 时,求函数
时,求函数 的单调区间.
的单调区间.(2)当
 时,讨论函数
时,讨论函数 与
与 图象的交点个数.
图象的交点个数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=
 ,下列结论中错误的是
,下列结论中错误的是A.

 , f(
, f( )=0
)=0B. 函数y=f(x)的图像是中心对称图形
C. 若
 是f(x)的极小值点,则f(x)在区间(-∞,
是f(x)的极小值点,则f(x)在区间(-∞, )单调递减
)单调递减D. 若
 是f(x)的极值点,则
是f(x)的极值点,则 (
( )=0
)=0 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知等差数列{an}的公差d≠0,且a1 , a3 , a13成等比数列,若a1=1,Sn是数列{an}前n项的和,则
 (n∈N+)的最小值为( )
(n∈N+)的最小值为( )
A.4
B.3
C.2 ﹣2
﹣2
D.
相关试题

