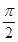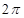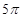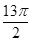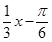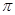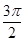(本题满分12分,每小题6分)
(1)若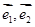 为基底向量,且
为基底向量,且 若A、B、D三点共线,求实数k的值;
若A、B、D三点共线,求实数k的值;
(2)用“五点作图法”在已给坐标系中画出函数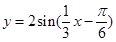 一个周期内的简图,并指出该函数图象是由函数
一个周期内的简图,并指出该函数图象是由函数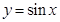 的图象进行怎样的变换而得到的?
的图象进行怎样的变换而得到的?
【答案】
(1)k=2; (2)把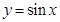 的图象向右平移
的图象向右平移 个单位长度,得到
个单位长度,得到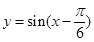 的图象;再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到
的图象;再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到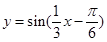 的图象;再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到函数
的图象;再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到函数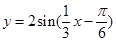 的图象;
的图象;
【解析】本试题主要是考查了三点共线以及三角函数的图像变换的综合运用。
(1)因为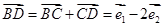 ,设
,设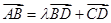 ,那么则有
,那么则有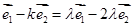 ,利用平面向量基本定理得到结论。
,利用平面向量基本定理得到结论。
(2)运用五点作图法得到函数图像,并结合图像变换得到结论。
解:(1)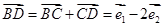 ,…………………………2分
,…………………………2分
设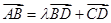 ,……………………………3分
,……………………………3分
得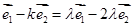 …………………………………4分
…………………………………4分
得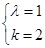 ,即k=2;…………………6分
,即k=2;…………………6分
(2)列表为
|
x |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
y |
0 |
2 |
0 |
-2 |
0 |
………………………2分
把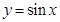 的图象向右平移
的图象向右平移 个单位长度,得到
个单位长度,得到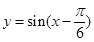 的图象;再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到
的图象;再把后者所有点的横坐标伸长到原来的3倍(纵坐标不变),得到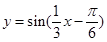 的图象;再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到函数
的图象;再把所得图象上所有点的纵坐标伸长到原来的2倍(横坐标不变)而得到函数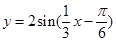 的图象;
的图象;
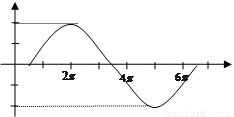 …………………4分
…………………4分