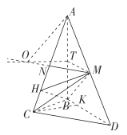
【题目】如图，在三棱锥中，平面，，，M为中点，H为线段上一点（除的中点外），且.当三棱锥的体积最大时，则三棱锥的外接球表面积为（ ）

A.B.

C.D.

【答案】B

【解析】

利用线面垂直的判定定理和性质，可以证明平面，利用三棱锥的等积性，结合基本不等式，这样可以求出，过点C作，取，的中点T，N，连接，，过点T作的平行线交于点O.利用线面垂直的性质和判定定理可以证明出O为三棱锥的外接球的球心，运用正切函数的定义，球的表面积公式进行求解即可.

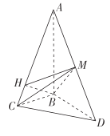
在中，因为M为中点，故，且，因为，，所以平面，故，又因为，所以平面，因此，故平面，三棱锥的体积等于三棱锥的体积，即只需底面面积最大即可.因为，则，故，当且仅当时取等号.在中，，故，过点C作，取，的中点T，N，连接，，过点T作的平行线交于点O.由平面知平面.又平面，故平面.因此O为三棱锥的外接球的球心，由，因为，所以，故，即三棱锥的外接球表面积为.

故选：B

关闭