【题目】已知等差数列{an}的公差d>0,则下列四个命题: ①数列{an}是递增数列;
②数列{nan}是递增数列;
③数列 ![]() 是递增数列;
是递增数列;
④数列{an+3nd}是递增数列;
其中正确命题的个数为( )
A.1
B.2
C.3
D.4
参考答案:
【答案】B
【解析】解:∵对于公差d>0的等差数列{an},an+1﹣an=d>0,∴数列{an}是递增数列成立,是真命题. 对于数列数列{nan},第n+1项与第n项的差等于 (n+1)an+1﹣nan=nd+an+1 , 不一定是正实数,故是假命题.
对于数列 ![]() ,第n+1项与第n项的差等于
,第n+1项与第n项的差等于 ![]() ,不一定是正实数,故是假命题.
,不一定是正实数,故是假命题.
对于数列数列{an+3nd},第n+1项与第n项的差等于 an+1+3(n+1)d﹣an﹣3nd=4d>0,
故数列{an+3nd}是递增数列成立,是真命题.
故选:B.
【考点精析】解答此题的关键在于理解等差数列的性质的相关知识,掌握在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在等边△ABC中,
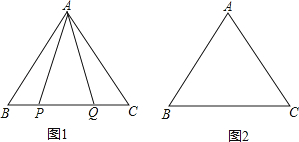
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系
 中,圆
中,圆 的方程为
的方程为 ,若直线
,若直线 上至少存在一点,使得以该点为圆心,1为半径的圆与圆
上至少存在一点,使得以该点为圆心,1为半径的圆与圆 有公共点,则
有公共点,则 的最大值为__________.
的最大值为__________. -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.

(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为 ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】
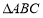 的内角
的内角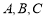 的对边分别为
的对边分别为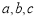 ,已知
,已知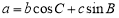
(1)求
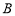 ;
;(2)若
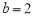 ,求
,求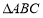 面积的最大值.
面积的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题满分12分)
在如图所示的多面体中,四边形
 和
和 都为矩形。
都为矩形。
(Ⅰ)若
 ,证明:直线
,证明:直线 平面
平面 ;
;(Ⅱ)设
 ,
,  分别是线段
分别是线段 ,
,  的中点,在线段
的中点,在线段 上是否存在一点
上是否存在一点 ,使直线
,使直线 平面
平面 ?请证明你的结论。
?请证明你的结论。 -
科目: 来源: 题型:
查看答案和解析>>【题目】设椭圆
 :
:  的离心率与双曲线
的离心率与双曲线 的离心率互为倒数,且椭圆的长轴长为4.
的离心率互为倒数,且椭圆的长轴长为4.(1)求椭圆
 的标准方程;
的标准方程;(2)若直线
 交椭圆
交椭圆 于
于 ,
,  两点,
两点,  (
( )为椭圆
)为椭圆 上一点,求
上一点,求 面积的最大值.
面积的最大值.
相关试题

