【题目】设函数![]() (
(![]() ,且
,且![]() ),
),![]() ,(其中
,(其中![]() 为
为![]() 的导函数).
的导函数).
(1)当![]() 时,求
时,求![]() 的极大值点;
的极大值点;
(2)讨论![]() 的零点个数.
的零点个数.
参考答案:
【答案】(1)![]() ;(2)详见解析.
;(2)详见解析.
【解析】试题分析:(1)令![]() 求出
求出![]() 的极值点,判断
的极值点,判断![]() 的符号变化即可得出答案;
的符号变化即可得出答案;
(2)对a和x进行讨论,利用零点的存在性定理,结合函数的图象判断零点的个数.
试题解析:
(1)![]() ,
,
当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,故
,故![]() 的极大值点为
的极大值点为![]() ;
;
(2)(i)先考虑![]() 时,
时, ![]() 的零点个数,当
的零点个数,当![]() 时,
时, ![]() 为单减函数,
为单减函数,
![]() ;
; ![]() ,由零点存在性定理知
,由零点存在性定理知![]() 有一个零点;
有一个零点;
当![]() 时,由
时,由![]() 得
得
![]() ,令
,令![]() ,则
,则![]() .
.
由![]() 得,
得, ![]() ,当
,当![]() 时,
时, ![]() ;当
;当![]() 时,
时, ![]() ,
,
故![]() ,
, ![]() ,且
,且![]() 总成立,故
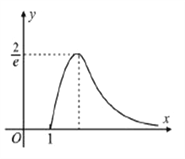
总成立,故![]() 的图像如下图,
的图像如下图,
由数形结合知,
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 无零点,故
无零点,故![]() 时,
时, ![]() 有一个零点;
有一个零点;
②若![]() 即
即![]() 时,当
时,当![]() 时,
时, ![]() 有一个零点,故
有一个零点,故![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③若![]() 即
即![]() ,当
,当![]() 时,
时, ![]() 有
有![]() 个零点,故
个零点,故![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
(ii)再考虑![]() 的情形,若
的情形,若![]() ,则
,则![]() ,同上可知,
,同上可知,
当![]() 即
即![]() 时,
时, ![]() 有一个零点;
有一个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
当![]() 即
即![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
综合上述,
①当![]() 或
或![]() 时,
时, ![]() 有一个零点;
有一个零点;
②当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点;
个零点;
③当![]() 或
或![]() 时,
时, ![]() 有
有![]() 个零点.
个零点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】命题
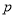 :已知实数
:已知实数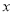 ,
, 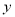 满足约束条件
满足约束条件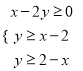 ,二元一次不等式
,二元一次不等式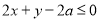 恒成立,
恒成立,命题
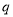 :设数列
:设数列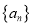 的通项公式为
的通项公式为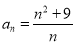 ,若
,若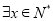 ,使得
,使得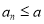 .
.(1)分别求出使命题
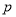 ,
, 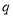 为真时,实数
为真时,实数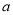 的取值范围;
的取值范围;(2)若命题
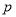 与
与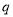 真假相同,求实数
真假相同,求实数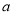 的取值范围.
的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】服装厂拟在2017年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)
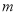 万件与年促销费用
万件与年促销费用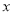 (
(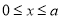 )万元满足
)万元满足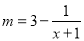 .已知
.已知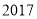 年生产该产品的固定投入为
年生产该产品的固定投入为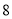 万元,每生产
万元,每生产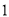 万件该产品需要投入
万件该产品需要投入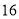 万元.厂家将每件产品的销售价格定为每件产品年平均成本的
万元.厂家将每件产品的销售价格定为每件产品年平均成本的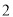 倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).
倍(产品成本包括固定投入和再投入两部分资金,不包括促销费用).(1)将2017年该产品的利润
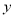 万元表示为年促销费用
万元表示为年促销费用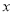 万元的函数;
万元的函数;(2)该服装厂2017年的促销费用投入多少万元时,利润最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方体ABCD﹣A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成角的余弦值为
-
科目: 来源: 题型:
查看答案和解析>>【题目】某手机卖场对市民进行国产手机认可度的调查,随机抽取
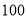 名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:
名市民,按年龄(单位:岁)进行统计和频数分布表和频率分布直线图如下:分组(岁)
频数

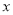

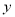
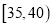
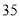
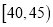
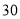
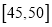
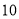
合计
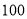
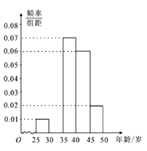
(1)求频率分布表中
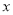 、
、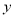 的值,并补全频率分布直方图;
的值,并补全频率分布直方图;(2)在抽取的这
 名市民中,按年龄进行分层抽样,抽取
名市民中,按年龄进行分层抽样,抽取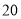 人参加国产手机用户体验问卷调查,现从这
人参加国产手机用户体验问卷调查,现从这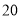 人中随机选取
人中随机选取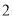 人各赠送精美礼品一份,设这
人各赠送精美礼品一份,设这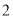 名市民中年龄在
名市民中年龄在 内的人数
内的人数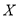 ,求
,求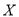 的分布列及数学期望.
的分布列及数学期望. -
科目: 来源: 题型:
查看答案和解析>>【题目】 (本小题满分12分)
如图, 在四面体ABOC中,
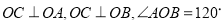 , 且
, 且 .
.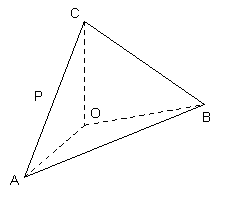
(Ⅰ)设为
 为
为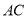 的中点, 证明: 在
的中点, 证明: 在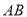 上存在一点
上存在一点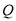 ,使
,使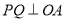 ,并计算
,并计算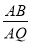 ;
;(Ⅱ)求二面角
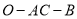 的平面角的余弦值。
的平面角的余弦值。 -
科目: 来源: 题型:
查看答案和解析>>【题目】为加快新能源汽车产业发展,推进节能减排,国家对消费者购买新能源汽车给予补贴,其中对纯电动乘车补贴标准如下表:

某校研究性学习小组,从汽车市场上随机选取了
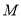 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程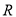 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(1)求
 的值;
的值;(2)若从这
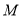 辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;
辆纯电动乘用车中任选3辆,求选到的3辆车续驶里程都不低于180公里的概率;(3)如果以频率作为概率,若某家庭在某汽车销售公司购买了2辆纯电动乘用车,设该家庭获得的补贴为
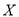 (单位:万元),求
(单位:万元),求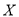 的分布列和数学期望
的分布列和数学期望 .
.
相关试题

