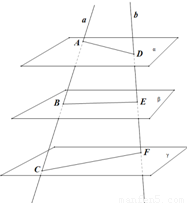
 如图,已知平面α∥β∥γ,直线a,b分别交α,β,γ于点A,B,C和D,E,F,
如图,已知平面α∥β∥γ,直线a,b分别交α,β,γ于点A,B,C和D,E,F,(1)求证:
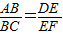 ;
;(2)若AB=1,BC=2,AD=3,CF=6,当AD与CF所成的角为60时,求BE的长.
【答案】分析:(1)连接AF,交β于点G,则点A,B,C,G共面,由β∥α,面ACF∩β=BG,面ACF∩γ=CF,知BG∥CF,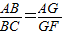 ,同理,
,同理,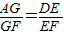 ,由此能够证明
,由此能够证明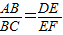 .
.
(2)连接BG,EG,由AB=1,BC=2,CF=6,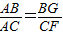 ,知BG=2,由
,知BG=2,由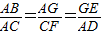 ,AD=3,知GE=2,再由AD与CF所成的角为60°,知∠BGE=60°或∠BGE=120°,由此能求出BE.
,AD=3,知GE=2,再由AD与CF所成的角为60°,知∠BGE=60°或∠BGE=120°,由此能求出BE.
解答: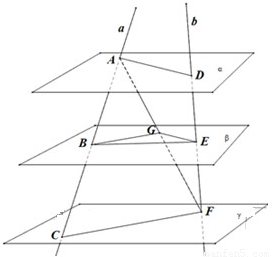 解:(1)连接AF,交β于点G,则点A,B,C,G共面,
解:(1)连接AF,交β于点G,则点A,B,C,G共面,
∵β∥α,面ACF∩β=BG,面ACF∩γ=CF,
∴BG∥CF,∴△ABG∽△ACF,
∴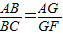 ,
,
同理,有AD∥GE,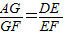 ,
,
∴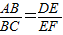 .
.
(2)∵α∥β∥γ,AD⊂α,CF⊂γ,
且AD与CF所成的角为60,
∴AD与CF是异面直线.
连接BG,EG,
∵AB=1,BC=2,CF=6,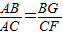 ,∴BG=2,
,∴BG=2,
∵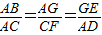 ,AD=3,∴GE=2,
,AD=3,∴GE=2,
∵AD与CF所成的角为60°,∴∠BGE=60°或∠BGE=120°,
当∠BGE=60°时,△BGE为等边三角形,此时BE=2,
当∠BGE=120°时,BE2=BG2+GE2-2BG•GE•cos120°=12,
此时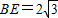 ,综上所述,
,综上所述,
BE=2或BE= .
.
点评:本题考查线段成比例的证明,考查线段长的求法,解题时要认真审题,仔细解答.
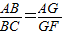 ,同理,
,同理,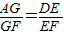 ,由此能够证明
,由此能够证明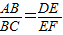 .
.(2)连接BG,EG,由AB=1,BC=2,CF=6,
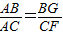 ,知BG=2,由
,知BG=2,由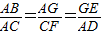 ,AD=3,知GE=2,再由AD与CF所成的角为60°,知∠BGE=60°或∠BGE=120°,由此能求出BE.
,AD=3,知GE=2,再由AD与CF所成的角为60°,知∠BGE=60°或∠BGE=120°,由此能求出BE.解答:
 解:(1)连接AF,交β于点G,则点A,B,C,G共面,
解:(1)连接AF,交β于点G,则点A,B,C,G共面,∵β∥α,面ACF∩β=BG,面ACF∩γ=CF,
∴BG∥CF,∴△ABG∽△ACF,
∴
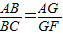 ,
,同理,有AD∥GE,
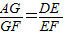 ,
,∴
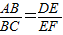 .
.(2)∵α∥β∥γ,AD⊂α,CF⊂γ,
且AD与CF所成的角为60,
∴AD与CF是异面直线.
连接BG,EG,
∵AB=1,BC=2,CF=6,
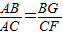 ,∴BG=2,
,∴BG=2,∵
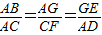 ,AD=3,∴GE=2,
,AD=3,∴GE=2,∵AD与CF所成的角为60°,∴∠BGE=60°或∠BGE=120°,
当∠BGE=60°时,△BGE为等边三角形,此时BE=2,
当∠BGE=120°时,BE2=BG2+GE2-2BG•GE•cos120°=12,
此时
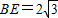 ,综上所述,
,综上所述,BE=2或BE=
 .
.点评:本题考查线段成比例的证明,考查线段长的求法,解题时要认真审题,仔细解答.

