【题目】在锐角△ABC中，a＝2，_______，求△ABC的周长l的范围．

在①(﹣cos，sin)，(cos，sin)，且，②cosA(2b﹣c)＝acosC，③f(x)＝cosxcos(x)，f(A)

注：这三个条件中任选一个，补充在上面问题中并对其进行求解．

【答案】l△ABC∈(6+2，6]．

【解析】

选①时，由平面向量的数量积与三角恒等变换求出A的值，再利用正弦定理和三角恒等变换求出△ABC周长的取值范围；

选②时，由正弦定理和三角恒等变换求出A的值，再利用正弦定理和三角恒等变换求出△ABC周长的取值范围；

选③时，由三角恒等变换求得A的值，再利用正弦定理和三角恒等变换求出△ABC周长的取值范围．

解：若选①，则由(﹣cos，sin)，(cos，sin)，且，

得，∴cosA，

又A∈(0，)，

所以A；

又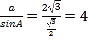，所以，，

△ABC的周长为，

即；

因为锐角△ABC中，A，所以，，

所以B∈(，)，

所以B∈(，)，

所以△ABC的周长为l△ABC∈(6+2，6]．

若选②，由cos A(2b﹣c)＝acos C，

所以2bcosA＝acosC+ccosA，

所以2sinBcosA＝sinAcosC+cosAsinC＝sin(A+C)＝sinB；

又B∈(0，π)，所以sinB≠0，所以cosA；

又A∈(0，)，所以A；

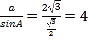又，所以，，

△ABC的周长为，

即；

因为锐角△ABC中，A，所以，，

所以B∈(，)，

所以B∈(，)，

所以△ABC的周长为l△ABC∈(6+2，6]．

若选③，则f(x)＝cos xcos(x)

cos xsin x

(cos2xsin2x)

sin(2x)，

又f(A)，所以sin(2A)，

又A∈(0，)，所以A；

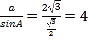又，所以，，

△ABC的周长为，

即；

因为锐角△ABC中，A，所以，，

所以B∈(，)，

所以B∈(，)，

所以△ABC的周长为l△ABC∈(6+2，6]．

关闭