【题目】
如图,在四棱锥P—ABCD中,平面PAD⊥底面ABCD,其中底面ABCD为等腰梯形,AD∥BC,
PA=AB=BC=CD=2,PD=2![]() ,PA⊥PD,Q为PD的中点.
,PA⊥PD,Q为PD的中点.
(Ⅰ)证明:CQ∥平面PAB;
(Ⅱ)求三棱锥Q-ACD的体积。

参考答案:
【答案】(Ⅰ)见解析;(Ⅱ)1.
【解析】试题分析:(Ⅰ)取PA的中点N,连接QN,BN.结合所给条件判断四边形![]() 为平行四边形,可得
为平行四边形,可得![]() ,再由线线平面可证线面平行;(Ⅱ)利用三棱锥的体积公式
,再由线线平面可证线面平行;(Ⅱ)利用三棱锥的体积公式![]() .可得结果.
.可得结果.
试题解析:(Ⅰ)证明 如图所示,取PA的中点N,连接QN,BN.
在△PAD中,PN=NA,PQ=QD,
所以QN∥AD,且QN=![]() AD.
AD.
在△APD中,PA=2,PD=2![]() ,PA⊥PD,
,PA⊥PD,
所以AD=![]() =4,而BC=2,所以BC=
=4,而BC=2,所以BC=![]() AD.
AD.
又BC∥AD,所以QN∥BC,且QN=BC,
故四边形BCQN为平行四边形,所以BN∥CQ.
又BN平面PAB,且CQ![]() 平面PAB, 所以CQ∥平面PAB.
平面PAB, 所以CQ∥平面PAB.
(Ⅱ)V=1
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了得到函数
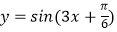 的图象,只需把函数y=sin3x的图象( )
的图象,只需把函数y=sin3x的图象( )
A.向左平移
B.向左平移
C.向右平移
D.向右平移
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线l过点P(﹣2,1),
(1)若直线l与直线x+y﹣1=0平行,求直线l的方程;
(2)若点A(﹣1,﹣2)到直线l的距离为1,求直线l的方程. -
科目: 来源: 题型:
查看答案和解析>>【题目】函数f(x)=
 sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)对任意x∈R,都有f(﹣x)+f(x)=0,f(x)+f(x+
sin(ωx+φ)﹣cos(ωx+φ)(0<φ<π,ω>0)对任意x∈R,都有f(﹣x)+f(x)=0,f(x)+f(x+  )=0,则f(
)=0,则f(  )=( )
)=( )
A.0
B.1
C.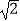
D.2 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=2
 sinxcosx+1﹣2sin2x,x∈R.
sinxcosx+1﹣2sin2x,x∈R.
(1)求函数f(x)的最小正周期和单调递增区间;
(2)将函数y=f(x)的图象上各点的纵坐标保持不变,横坐标缩短到原来的 ,把所得到的图象再向左平移
,把所得到的图象再向左平移  单位,得到的函数y=g(x)的图象,求函数y=g(x)在区间
单位,得到的函数y=g(x)的图象,求函数y=g(x)在区间 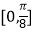 上的最小值.
上的最小值. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知单调递增的等比数列{an}满足:a2+a3+a4=28,且a3+2是a2 , a4的等差中项.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)设bn=anlog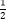 an , 求数列{bn}的前n项和Sn .
an , 求数列{bn}的前n项和Sn . -
科目: 来源: 题型:
查看答案和解析>>【题目】假设小明订了一份报纸,送报人可能在早上6:30—7:30之间把报纸送到,小明离家的时间在早上7:00—8:00之间,则他在离开家之前能拿到报纸的概率( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

