在首项为81,公差为-7的等差数列{an}中,最接近零的是第____项.
- A.11
- B.12
- C.13
- D.14
C
分析:由a1=81,d=-7,得到an=81+(n-1)×(-7)=88-7n,由an=88-7n≥0,能求出最接近零的项.
解答:∵a1=81,d=-7,
∴an=81+(n-1)×(-7)=88-7n,
由an=88-7n≥0,
解得n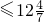 ,
,
∴最接近零的是第13项,
故选C.
点评:本题考查等差数列的通项公式,解题时要认真审题,仔细解答,是基础题.
分析:由a1=81,d=-7,得到an=81+(n-1)×(-7)=88-7n,由an=88-7n≥0,能求出最接近零的项.
解答:∵a1=81,d=-7,
∴an=81+(n-1)×(-7)=88-7n,
由an=88-7n≥0,
解得n
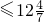 ,
,∴最接近零的是第13项,
故选C.
点评:本题考查等差数列的通项公式,解题时要认真审题,仔细解答,是基础题.

