【题目】对于命题![]() :存在一个常数
:存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() 恒成立.
恒成立.
(1)试给出这个常数![]() 的值;
的值;
(2)在(1)所得结论的条件下证明命题![]() ;
;
(3)对于上述命题,某同学正确地猜想了命题![]() :“存在一个常数
:“存在一个常数![]() ,使得不等式
,使得不等式![]() 对任意正数
对任意正数![]() ,
,![]() ,
,![]() 恒成立.”观察命题
恒成立.”观察命题![]() 与命题
与命题![]() 的规律,请猜想与正数
的规律,请猜想与正数![]() ,
,![]() ,
,![]() ,
,![]() 相关的命题.
相关的命题.
参考答案:
【答案】(1) ![]() ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
【解析】试题分析:(1)取特值,定常数![]() 的值;(2)利用分析法证明命题P;(3).猜想结论:存在一个常数
的值;(2)利用分析法证明命题P;(3).猜想结论:存在一个常数![]() ,使得不等式
,使得不等式
![]()
对任意正数![]() ,
,![]() ,
,![]() ,
,![]() 恒成立.
恒成立.
试题解析:
(1)令![]() 得:
得:![]() ,故
,故![]() ;
;
(2)先证明![]() .
.
∵![]() ,
,![]() ,要证上式,只要证
,要证上式,只要证![]() ,
,
即证![]() 即证
即证![]() ,这显然成立.
,这显然成立.
∴![]() .
.
再证明![]() .
.
∵![]() ,
,![]() ,要证上式,只要证
,要证上式,只要证![]() ,
,
即证![]() 即证
即证![]() ,这显然成立.
,这显然成立.
∴![]() .
.
(3)猜想结论:存在一个常数,使得不等式
![]()
对任意正数![]() ,
,![]() ,
,![]() ,
,![]() 恒成立.
恒成立.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
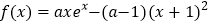 (其中
(其中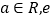 为自然对数的底数,
为自然对数的底数,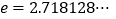 ).
).(1)若
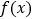 仅有一个极值点,求
仅有一个极值点,求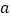 的取值范围;
的取值范围;(2)证明:当
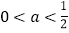 时,
时,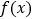 有两个零点
有两个零点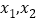 ,且
,且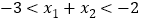 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】设集合A={x|-2≤x≤5},B={x|m+1≤x≤2m-1}.
(1)若BA,求实数m的取值范围;
(2)当x∈R时,不存在元素x使x∈A与x∈B同时成立,求实数m的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】设函数f(x)=|2x-1|+|2x-a|+a,x∈R.
(1)当a=3时,求不等式f(x)>7的解集;
(2)对任意x∈R恒有f(x)≥3,求实数a的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.
(a>0,a≠1,m≠﹣1),是定义在(﹣1,1)上的奇函数.(I)求f(0)的值和实数m的值;
(II)当m=1时,判断函数f(x)在(﹣1,1)上的单调性,并给出证明;
(III)若
 且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围.
且f(b﹣2)+f(2b﹣2)>0,求实数b的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数f(x)=loga
 (其中a>0,且a≠1).
(其中a>0,且a≠1).(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性并给出证明;
(3)若x∈
 时,函数f(x)的值域是[0,1],求实数a的值.
时,函数f(x)的值域是[0,1],求实数a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】设函数
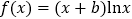 ,
, ,已知曲线
,已知曲线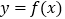 在点
在点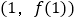 处的切线与直线
处的切线与直线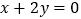 垂直.
垂直.(1)求
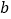 的值;
的值;(2)若对任意
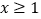 ,都有
,都有 ,求
,求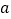 的取值范围.
的取值范围.
相关试题

