
【题目】世界那么大,我想去看看,处在具有时尚文化代表的大学生们旅游动机强烈,旅游可支配收入日益增多,可见大学生旅游是一个巨大的市场.为了解大学生每年旅游消费支出(单位:百元)的情况,相关部门随机抽取了某大学的![]() 名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
名学生进行问卷调查,并把所得数据列成如下所示的频数分布表:
组别 |
|
|
|
|
|
频数 |
|
|
|
|
|
(Ⅰ)求所得样本的中位数(精确到百元);
(Ⅱ)根据样本数据,可近似地认为学生的旅游费用支出![]() 服从正态分布
服从正态分布![]() ,若该所大学共有学生
,若该所大学共有学生![]() 人,试估计有多少位同学旅游费用支出在
人,试估计有多少位同学旅游费用支出在![]() 元以上;
元以上;
(Ⅲ)已知样本数据中旅游费用支出在![]() 范围内的
范围内的![]() 名学生中有
名学生中有![]() 名女生,
名女生, ![]() 名男生,现想选其中
名男生,现想选其中![]() 名学生回访,记选出的男生人数为
名学生回访,记选出的男生人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
附:若![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
 星级口算天天练系列答案
星级口算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]()
(![]() )求数列
)求数列![]() 的通项公式;
的通项公式;
(![]() )若数列
)若数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(![]() )在(
)在(![]() )的条件下,设
)的条件下,设![]() ,问是否存在实数
,问是否存在实数![]() 使得数列
使得数列![]() 是单调递增数列?若存在,求出
是单调递增数列?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“微信运动”是手机![]() 推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有
推出的多款健康运动软件中的一款,杨老师的微信朋友圈内有![]() 位好友参与了“微信运动”,他随机选取了
位好友参与了“微信运动”,他随机选取了![]() 位微信好友(女
位微信好友(女![]() 人,男
人,男![]() 人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
人),统计其在某一天的走路步数.其中,女性好友的走路步数数据记录如下:
5860 8520 7326 6798 7325 8430 3216 7453 11754 9860
8753 6450 7290 4850 10223 9763 7988 9176 6421 5980
男性好友走路的步数情况可分为五个类别: ![]() 步)(说明:“
步)(说明:“![]() ”表示大于等于
”表示大于等于![]() ,小于等于
,小于等于![]() .下同),
.下同), ![]() 步),
步), ![]() 步),
步), ![]() 步),
步), ![]() 步及以
步及以![]() ),且
),且![]() 三种类别人数比例为
三种类别人数比例为![]() ,将统计结果绘制如图所示的条形图.
,将统计结果绘制如图所示的条形图.

若某人一天的走路步数超过![]() 步被系统认定为“卫健型",否则被系统认定为“进步型”.
步被系统认定为“卫健型",否则被系统认定为“进步型”.
(1)若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的![]() 名好友中,每天走路步数在
名好友中,每天走路步数在![]() 步的人数;
步的人数;
(2)请根据选取的样本数据完成下面的![]() 列联表并据此判断能否有
列联表并据此判断能否有![]() 以上的把握认定“认定类型”与“性别”有关?
以上的把握认定“认定类型”与“性别”有关?
卫健型 | 进步型 | 总计 | |
男 | 20 | ||
女 | 20 | ||
总计 | 40 |
(3)若从杨老师当天选取的步数大于10000的好友中按男女比例分层选取![]() 人进行身体状况调查,然后再从这
人进行身体状况调查,然后再从这![]() 位好友中选取
位好友中选取![]() 人进行访谈,求至少有一位女性好友的概率.
人进行访谈,求至少有一位女性好友的概率.
附:  ,
,
| 0.10 | 0.05 | 0.025 | 0.010 |
| 2.706 | 3.841 | 5.024 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市为了解游客人数的变化规律,提高旅游服务质量,收集并整理了2014年1月至2016年12月期间月接待游客量(单位:万人)的数据,绘制了如图所示的折线图.根据该折线图,下列结论错误的是( )
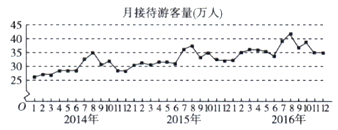
A.月接待游客量逐月增加
B.年接待游客量逐年增加
C.各年的月接待游客量高峰期大致在7,8月
D.各年1月至6月的月接待游客量相对于7月至12月,波动性更小,变化比较平稳
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面上动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() ,记动点
,记动点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(1)求曲线![]() 的方程;
的方程;
(2)设![]() 是曲线
是曲线![]() 上的动点,直线
上的动点,直线![]() 的方程为
的方程为![]() .
.
①设直线![]() 与圆
与圆![]() 交于不同两点
交于不同两点![]() ,
, ![]() ,求
,求![]() 的取值范围;
的取值范围;
②求与动直线![]() 恒相切的定椭圆
恒相切的定椭圆![]() 的方程;并探究:若
的方程;并探究:若![]() 是曲线
是曲线![]() :
: ![]() 上的动点,是否存在直线
上的动点,是否存在直线![]() :
: ![]() 恒相切的定曲线
恒相切的定曲线![]() ?若存在,直接写出曲线
?若存在,直接写出曲线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
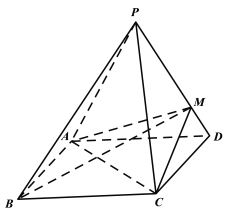
【题目】如图,四棱锥P-ABCD的底面是矩形,侧面PAD为等边三角形,AB=![]() ,AD=
,AD=![]() , PB=
, PB=![]() .
.
(1)求证:平面PAD⊥平面ABCD;
(2)M是棱PD上一点,三棱锥M-ABC的体积为1.记三棱锥P-MAC的体积为![]() ,三棱锥M-ACD的体积为
,三棱锥M-ACD的体积为![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设△ABC三个内角A、B、C所对的边分别为![]() 已知
已知![]()
(1)求角B的大小;
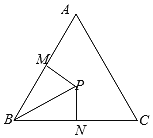
(2)如图,在△ABC内取一点P,使得PB=2,过点P分别作直线BA、BC的垂线PM、PN,垂足分别是M、N,设∠PBA=![]() 求四边形PMBN的面积的最大值及此时
求四边形PMBN的面积的最大值及此时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com